题目内容
1．已知函数f（x）=ax2-x+a，a∈R，（1）当a=2时，解不等式f（x）＞3；
（2）若函数f（x）有最大值-2，求实数a的值．
分析 （1）代入a值，解二次不等式即可；
（2）根据二次函数的性质直接求解即可．
解答 解：（1）当a=2时，f（x）=ax2-x+a，
由f（x）＞3得2x2-x+2＞3 …（2分）
解得$x＜-\frac{1}{2}$或x＞1…（4分）
故不等式的解集为 （-∞，$-\frac{1}{2}$∪（1，+∞）（5分）
（2）二次函数有最大值，必须a＜0…（6分）
由$\frac{{4{a^2}-1}}{4a}=-2$得4a2+8a-1=0，
解得$a=-1±\frac{{\sqrt{5}}}{2}$…（9分）
由于a＜0，故实数$a=-1-\frac{{\sqrt{5}}}{2}$…（10分）
点评 考查了二次不等式和二次函数的基本性质，属于基础题型，应熟练掌握．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
相关题目
9．
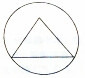棱长为a的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，并且图中三角形（正四面体的截面）的面积是3$\sqrt{2}$，则a等于（ ）
棱长为a的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，并且图中三角形（正四面体的截面）的面积是3$\sqrt{2}$，则a等于（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$ |
16．已知数列{an}是等差数列，若a1-a9+a17=7，则a3+a15=（ ）
| A． | 7 | B． | 14 | C． | 21 | D． | 7（n-1） |
6．将函数f（x）=sin2x的图象向右平移$\frac{π}{4}$个单位长度后得到函数g（x）的图象，则下列说法正确的是（ ）
| A． | g（x）在（0，$\frac{π}{4}$）上单调递增，且为奇函数 | |
| B． | g（x）的最大值为1，其图象关于直线x=$\frac{π}{2}$对称 | |
| C． | g（x）在（-$\frac{3π}{8}$，$\frac{π}{8}$）上单调递增，且为偶函数 | |
| D． | g（x）的周期为π，其图象关于点（$\frac{3π}{8}$，0）对称 |
13．△ABC的三个内角分别记为A，B，C，若tanAtanB=tanA+tanB+1，则cosC的值是（ ）
| A． | -$\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
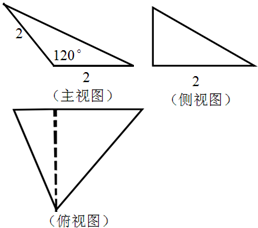某几何体的三视图如图，则该几何体的外接球表面积20π．