解关于x的不等式:ax2+4＞2x+2ax．题目和参考答案——青夏教育精英家教网—

题目内容

14．解关于x的不等式：ax²+4＞2x+2ax（0≤a＜2）．

分析对a的大小关系分类讨论，利用一元二次不等式的解法即可得出．

解答解：原不等式化为（x-2）（ax-2）＞0，
①当a=0时，原不等式化为x-2＜0，解得x＜2；
②当0＜a＜1时，原不等式化为$（x-2）（x-\frac{2}{a}）＞0$，且$2＜\frac{2}{a}$，
解得$x＞\frac{2}{a}$或x＜2；
③当a=1时，原不等式化为（x-2）²＞0，解得x∈R且x≠2；
④当1＜a＜2时，原不等式化为$（x-2）（x-\frac{2}{a}）＞0$，且$2＞\frac{2}{a}$，
解得$x＜\frac{2}{a}$或x＞2；
综上所述，当a=0时，原不等式的解集为{x|x＜2}；
当0＜a≤1时，原不等式的解集为$\left\{{x|}\right.x＞\frac{2}{a}$或x＜2}；
当1＜a＜2时，原不等式的解集为{x|x＞2或$x＜\frac{2}{a}\left.{\;}\right\}$．

点评本题考查了一元二次不等式的解法，考查了分类讨论的思想方法，属于中档题．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

13．目前，在“互联网+”和“大数据”浪潮的推动下，在线教育平台如雨后春笋般蓬勃发展，与此同时好多学生家长和相关专家对在线教学也产生了质疑，主要原因就是在线上教学，学生是否能认真听讲，在这种情况下，我市教育主管部门在我市各中小学采用分层抽样的方式抽出15周岁以下和15周岁以上各200人进行调查研究，其中15周岁以下的能认真听讲的150人，不能做到认真听讲的50人，15周岁以上的170人能认真听讲，不能做到认真听讲的30人，根据以上数据完成下列各题：
（1）完成下列2×2列联表

	不认真听讲	能认真听讲	总计
15周岁以下
15周岁以上
总计

（2）请说明是否有97.5%以上的把握认为能否认真听见与年龄有关？
（3）现用分层抽样的方法，从15周岁以下的人种抽取8人，在这8人中任取两人进行座谈，求抽到的人中至少有一人能认真听讲的概率．
参考公式：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，（n=a+b+c+d）

P（K²≥k₀）	0.05	0.025	0.010	0.005	0.001
k0	3.841	5.024	6.635	7.879	10.828

2．设集合P₁={x|x²+ax+1＞0}，P₂={x|x²+ax+2＞0}，Q₁={x|x²+x+b＞0}，Q₂={x|x²+2x+b＞0}，其中a，b∈R，下列说法正确的是（　　）

	A．	对任意a，P₁是P₂的子集，对任意b，Q₁不是Q₂的子集
	B．	对任意a，P₁是P₂的子集，存在b，使得Q₁是Q₂的子集
	C．	存在a，P₁不是P₂的子集，对任意b，Q₁不是Q₂的子集
	D．	存在a，P₁不是P₂的子集，存在b，使得Q₁是Q₂的子集

9．

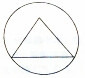棱长为a的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，并且图中三角形（正四面体的截面）的面积是3$\sqrt{2}$，则a等于（　　）

19．已知直线ax+y+2=0与直线x-（3a-1）y-1=0互相垂直，则a=$\frac{1}{2}$．

6．将函数f（x）=sin2x的图象向右平移$\frac{π}{4}$个单位长度后得到函数g（x）的图象，则下列说法正确的是（　　）

	A．	g（x）在（0，$\frac{π}{4}$）上单调递增，且为奇函数
	B．	g（x）的最大值为1，其图象关于直线x=$\frac{π}{2}$对称
	C．	g（x）在（-$\frac{3π}{8}$，$\frac{π}{8}$）上单调递增，且为偶函数
	D．	g（x）的周期为π，其图象关于点（$\frac{3π}{8}$，0）对称

3．△ABC的内角A，B，C的对边分别为a，b，c，若a，b，c成等比数列，且c=2a，则cosB等于（　　）

4．复数z=$\frac{-3+i}{2+i}$的共轭复数为$\overline{z}$，则$\overline{z}$的虚部为-1．

试题分类