题目内容
18．已知tanα=3，计算：（Ⅰ）$\frac{4sinα-2cosα}{5cosα+3sinα}$；
（Ⅱ）sinα•cosα．
分析 （Ⅰ）分子、分母同除以cosα，利用同角三角函数基本关系式即可计算得解．
（Ⅱ）将分母看成1，即两弦值的平方和，由已知，利用同角三角函数基本关系式即可计算得解．
解答 （本题满分为12分）
解：（Ⅰ）∵tanα=3，
∴$\frac{4sinα-2cosα}{5cosα+3sinα}$=$\frac{4tanα-2}{5+3tanα}$=$\frac{4×3-2}{5+3×3}$=$\frac{5}{7}$．…（6分）
（Ⅱ）∵tanα=3，
∴sinα•cosα=$\frac{sinα•cosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{tanα}{ta{n}^{2}α+1}$=$\frac{3}{{3}^{2}+1}$=$\frac{3}{10}$．…（12分）
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．
练习册系列答案
相关题目
16．在极坐标系中，与点（3，-$\frac{π}{3}$）关于极轴所在直线对称的点的极坐标是（ ）
| A． | （3，$\frac{2π}{3}$） | B． | （3，$\frac{π}{3}$） | C． | （3，$\frac{4π}{3}$） | D． | （3，$\frac{5π}{6}$） |
9．
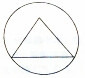棱长为a的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，并且图中三角形（正四面体的截面）的面积是3$\sqrt{2}$，则a等于（ ）
棱长为a的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，并且图中三角形（正四面体的截面）的面积是3$\sqrt{2}$，则a等于（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$ |
6．将函数f（x）=sin2x的图象向右平移$\frac{π}{4}$个单位长度后得到函数g（x）的图象，则下列说法正确的是（ ）
| A． | g（x）在（0，$\frac{π}{4}$）上单调递增，且为奇函数 | |
| B． | g（x）的最大值为1，其图象关于直线x=$\frac{π}{2}$对称 | |
| C． | g（x）在（-$\frac{3π}{8}$，$\frac{π}{8}$）上单调递增，且为偶函数 | |
| D． | g（x）的周期为π，其图象关于点（$\frac{3π}{8}$，0）对称 |
13．△ABC的三个内角分别记为A，B，C，若tanAtanB=tanA+tanB+1，则cosC的值是（ ）
| A． | -$\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
3．△ABC的内角A，B，C的对边分别为a，b，c，若a，b，c成等比数列，且c=2a，则cosB等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{\sqrt{2}}{3}$ |
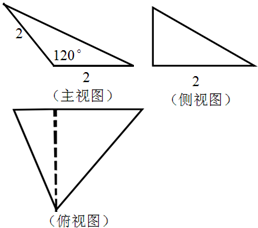某几何体的三视图如图，则该几何体的外接球表面积20π．