题目内容
7.用列举法表示下列集合.(1)A={y|y=-2x2+7,x∈N,y∈N};
(2)B={(x,y)|y=-2x2+7,x∈N,y∈N}.
分析 根据题意,分析可得符合集合中元素的特征的实数,用列举法表示可得答案.
解答 解:(1)A={y|y=-2x2+7,x∈N,y∈N}={5,7}
(2)B={(x,y)|y=-2x2+7,x∈N,y∈N}={(0,7),(1,5)}
点评 本题考查集合的表示方法,关键是分析出集合中元素的特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知复数z1=cosθ-i,z2=sinθ+i,则|z1•z2|的最大值为( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 3 |
15.已知函数f(x)=|2x-1|+|x-2a|,若?x∈[1,2],f(x)≤4,则实a的取值范围是( )
| A. | ($\frac{1}{4}$,$\frac{3}{2}$] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [1,$\frac{3}{2}$] | D. | [$\frac{1}{2}$,2] |
16.在极坐标系中,与点(3,-$\frac{π}{3}$)关于极轴所在直线对称的点的极坐标是( )
| A. | (3,$\frac{2π}{3}$) | B. | (3,$\frac{π}{3}$) | C. | (3,$\frac{4π}{3}$) | D. | (3,$\frac{5π}{6}$) |
9.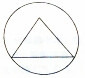 棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )
棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )
 棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )
棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
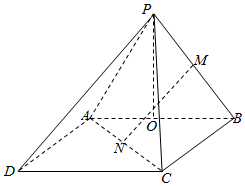 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,