题目内容
下列函数中，在其定义域内既是奇函数又是减函数的是（ ）
| A、y=-lnx | ||
B、y=x
| ||
| C、y=tanx | ||
| D、y=-x3-x |
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：根据奇函数定义域的特点，幂函数的单调性，正切函数的单调性，以及奇函数的定义及函数导数符号和函数单调性的关系即可找出正确选项．
解答：
解：y=-lnx不是奇函数，不符合条件；
y=x
是增函数，不符合条件；
y=tanx在定义域内不是单调函数；
y=-x3-x容易判断该函数为奇函数，且y′=-3x2-1＜0，所以该函数在R上是减函数，符合条件．
故选D．
y=x
| 1 |
| 3 |
y=tanx在定义域内不是单调函数；
y=-x3-x容易判断该函数为奇函数，且y′=-3x2-1＜0，所以该函数在R上是减函数，符合条件．
故选D．
点评：考查奇函数定义域的特点，幂函数的单调性，正切函数的单调性，以及函数导数符号和函数单调性的关系．
练习册系列答案
相关题目
已知数列{an}是公差不为零的等差数列，a1=2，且a2，a4，a8成等比数列．
（I）求数列{an}的通项；
（Ⅱ）设数列{bn-an}是等比数列，且b2=7，b5=91，求数列{bn}的前n项和Tn．
（I）求数列{an}的通项；
（Ⅱ）设数列{bn-an}是等比数列，且b2=7，b5=91，求数列{bn}的前n项和Tn．
已知数列{an}的首项为（0，-1），点（an，an+1）在函数x-y+2=0的图象上
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{an}的前n项之和为Sn，求
+
+
+…+
的值．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{an}的前n项之和为Sn，求
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
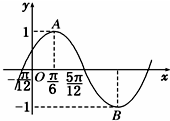函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
| A、y=sin 2x | ||
| B、y=cos 2x | ||
C、y=sin（2x+
| ||
D、y=sin（2x-
|
若关于实数x的不等式|x+1|+|x-2|＞a2-2a恒成立，则实数a的取值范围是（ ）
| A、（-1，3） |
| B、[-1，3] |
| C、（-∞，-1）∪（3，+∞） |
| D、（-∞，-1]∪[3，+∞） |
函数f（x）=
的单调增区间为（ ）
| x2-2x |
| A、（-∞，0] |
| B、[2，+∞） |
| C、[0，1] |
| D、[1，2] |