题目内容
4. 如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,∠ABC=60°,点D在PD上,且$\frac{PE}{ED}$=2.
如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,∠ABC=60°,点D在PD上,且$\frac{PE}{ED}$=2.(Ⅰ)求二面角E-AC-D的大小;
(Ⅱ)在棱PC上是否存在点F使得BF∥平面EAC?若存在,试求PF的值;若不存在,请说明理由.
分析 (Ⅰ)取BC中点G,连结AG,以A为原点,AG为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,求出平面ACE的法向量和平面ACD的法向量,利用向量法能求出二面角E-AC-D的大小.
(Ⅱ)设在棱PC上存在点F(a,b,c),且$\overrightarrow{PF}=λ\overrightarrow{PC}$,0≤λ≤1,使得BF∥平面EAC,求出平面ACE的法向量,利用向量法推导出在棱PC上不存在点F使得BF∥平面EAC.
解答 解:(Ⅰ) 取BC中点G,连结AG,
取BC中点G,连结AG,
∵在底面为菱形的四棱锥P-ABCD,中,PA⊥平面ABCD,PA=AB=1,∠ABC=60°,
∴AG⊥BD,AG=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
以A为原点,AG为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
则A(0,0,0),C($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),D(0,1,0),P(0,0,1),
∵点E在PD上,且$\frac{PE}{ED}$=2,∴E($0,\frac{2}{3},\frac{1}{3}$),
$\overrightarrow{AE}$=(0,$\frac{2}{3}$,$\frac{1}{3}$),$\overrightarrow{AC}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),
设平面ACE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=\frac{\sqrt{3}}{2}x+\frac{1}{2}y=0}\\{\overrightarrow{n}•\overrightarrow{AE}=\frac{2}{3}x+\frac{1}{3}z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-$\sqrt{3}$,-2),
平面ACD的法向量$\overrightarrow{m}$=(0,0,1),
设二面角E-AC-D的大小为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{8}}$=$\frac{\sqrt{2}}{2}$,∴θ=45°,
∴二面角E-AC-D的大小为45°.
(Ⅱ)设在棱PC上存在点F(a,b,c),且$\overrightarrow{PF}=λ\overrightarrow{PC}$,0≤λ≤1,使得BF∥平面EAC,
则(a,b,c-1)=($\frac{\sqrt{3}}{2}λ,\frac{1}{2}λ$,-λ),解得F($\frac{\sqrt{3}}{2}λ,\frac{1}{2}λ,1-λ$),
∵B($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),∴$\overrightarrow{BF}$=($\frac{\sqrt{3}}{2}λ-\frac{\sqrt{3}}{2}$,$\frac{1}{2}λ+\frac{1}{2}$,1-λ),
∵平面ACE的法向量$\overrightarrow{n}$=(1,-$\sqrt{3}$,-2),BF∥平面EAC,
∴$\overrightarrow{BF}•\overrightarrow{n}$=$\frac{\sqrt{3}}{2}λ-\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}λ-\frac{\sqrt{3}}{2}$-2+2λ=0,
解得λ=1+$\frac{\sqrt{3}}{2}$∉(0,1),
∴在棱PC上不存在点F使得BF∥平面EAC.
点评 本题考查二面角的大小的求法,考查满足线面平行的点是否存在的判断与求法,涉及到空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

 阅读快车系列答案
阅读快车系列答案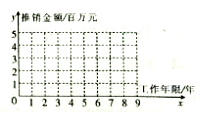 某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:
某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x(年) | 3 | 5 | 6 | 7 | 9 |
| 推销金额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若某推销员工作年限为11年,试估计他的年推销金额.
| A. | 5 | B. | 25 | C. | $\sqrt{41}$ | D. | 5$\sqrt{2}$ |
| A. | 方程x2+ax+b=0至多有一个实根 | B. | 方程x2+ax+b=0至少有一个实根 | ||
| C. | 方程x2+ax+b=0至多有两个实根 | D. | 方程x2+ax+b=0恰好有两个实根 |
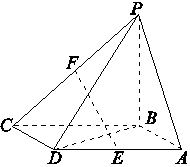 如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.
如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.