题目内容
19.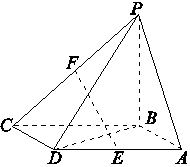 如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.
如图所示,四棱锥P ABCD的底面ABCD是平行四边形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分别是棱AD、PC的中点.(1)证明:EF∥平面PAB;
(2)求BD与PA所成角的大小.
分析 (1)取PB中点M,连接MF,AM.可得MF∥BC,且MF=$\frac{1}{2}$BC.再得MF∥AE且MF=AE,得四边形AMFE为平行四边形,即EF∥AM.证得EF∥平面PAB
(2)延长CD至N,使DN=CD,连接PN、AN,则由底面ABCD是平行四边形⇒AB$\underline{\underline{∥}}$DN⇒AN$\underline{\underline{∥}}$BD,所以∠PAN就是所求的角,求∠PAN即可
解答 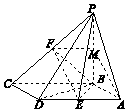 解:(1)证明:如图所示,取PB中点M,连接MF,AM.
解:(1)证明:如图所示,取PB中点M,连接MF,AM.
因为F为PC中点,所以MF∥BC,且MF=$\frac{1}{2}$BC.
由已知有BC∥AD,BC=AD,
又由于E为AD中点,因而MF∥AE且MF=AE,
故四边形AMFE为平行四边形,所以EF∥AM.
又AM?平面PAB,而EF?平面PAB,所以EF∥平面PAB.…(6分)
(2)延长CD至N,使DN=CD,连接PN、AN,则由底面ABCD是平行
四边形⇒AB$\underline{\underline{∥}}$DN⇒AN$\underline{\underline{∥}}$BD,所以∠PAN就是所求的角,
PD垂直平分CN$⇒PN=PC=\sqrt{7}⇒P{N^2}=P{A^2}+A{N^2}⇒∠PAN={90°}$
BD与PA所成的角为90°.…(12分)
点评 本题考查了线面平行、线线角,转化思想是解题关键,属于中档题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
14.若x,y满足约束条件$\left\{{\begin{array}{l}{x+y-2≥0}\\{x-y-2≤0}\\{2x-y-2≥0}\end{array}}\right.$,则z=x+2y的最小值为( )
| A. | $\frac{8}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | -4 |
20.函数f(x)=x2-4x+4的最小值是( )
| A. | 3 | B. | 0 | C. | -1 | D. | -2 |
 如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,∠ABC=60°,点D在PD上,且$\frac{PE}{ED}$=2.
如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,∠ABC=60°,点D在PD上,且$\frac{PE}{ED}$=2.