题目内容
5.用反证法证明命题“设a,b为实数,则方程x2+ax+b=0没有实数根”时,要做的假设是( )| A. | 方程x2+ax+b=0至多有一个实根 | B. | 方程x2+ax+b=0至少有一个实根 | ||
| C. | 方程x2+ax+b=0至多有两个实根 | D. | 方程x2+ax+b=0恰好有两个实根 |
分析 直接利用命题的否定写出假设即可.
解答 解:反证法证明问题时,反设实际是命题的否定,
∴用反证法证明命题“设a,b为实数,则方程x2+ax+b=0没有实数根”时,要做的假设是方程x2+ax+b=0至少有一个实根.
故选:B.
点评 本题考查反证法证明问题的步骤,基本知识的考查.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
5.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
(Ⅰ)在答题纸上列出这些数据的频率分布表,并作出频率分布直方图;
(Ⅱ)估计这种产品质量指标值的平均值及中位数(中位数的数值保留到小数点后一位).
| 质量指标 值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(Ⅱ)估计这种产品质量指标值的平均值及中位数(中位数的数值保留到小数点后一位).
13.关于直线a,b,c以及平面α,β,给出下列命题:
①若a∥α,b∥α,则a∥b
②若a∥α,b⊥α,则a⊥b
③若a?α,b?α,且c⊥a,c⊥b,则c⊥α
④若a⊥α,a∥β,则α⊥β
其中正确的命题是( )
①若a∥α,b∥α,则a∥b
②若a∥α,b⊥α,则a⊥b
③若a?α,b?α,且c⊥a,c⊥b,则c⊥α
④若a⊥α,a∥β,则α⊥β
其中正确的命题是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
20.函数f(x)=x2-4x+4的最小值是( )
| A. | 3 | B. | 0 | C. | -1 | D. | -2 |
10.不等式lnx+x-1<0的解集为( )
| A. | $(0,\frac{e}{4})$ | B. | $(0,\frac{e}{2})$ | C. | (0,1) | D. | (1,+∞) |
17.已知集合M={x|x(4-x)<0},N={x|(x-1)(x-6)<0,x∈Z},则M∩N=( )
| A. | (1,6) | B. | (4,6) | C. | {4,5,6} | D. | {5} |
15.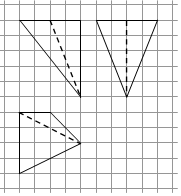 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )| A. | 15 | B. | 16 | C. | $\frac{50}{3}$ | D. | $\frac{53}{3}$ |
 如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,∠ABC=60°,点D在PD上,且$\frac{PE}{ED}$=2.
如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,∠ABC=60°,点D在PD上,且$\frac{PE}{ED}$=2.