Question

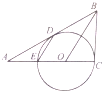如图，以Rt△ABC直角边AC上一点O为圆心，OC为半径的⊙O与AC另一个交点E，D为斜边AB上一点且在⊙O上，AD²=AE•AC．
（Ⅰ）证明AB是⊙O的切线；
（Ⅱ）若DE•OB=8，求⊙O的半径．

Answer 1

考点：与圆有关的比例线段,圆的切线的判定定理的证明

专题：综合题,立体几何

分析：（Ⅰ）连接OD，CD，证明∠ACD=∠ODC，利用CE是⊙O的直径，可得∠ODA=90°，即可确定AB是⊙O的切线；
（Ⅱ）证明△CDE∽△BCO，利用DE•OB=8，求⊙O的半径．

解答： （Ⅰ）证明：连接OD，CD，
∵AD²=AE•AC，
∴

AD

AE

=

AC

AD

，
又∵∠DAE=∠DAC，
∴△DAE∽△CAD，
∴∠ADE=∠ACD，
∵OD=OC，∴∠ACD=∠ODC，
又∵CE是⊙O的直径，
∴∠ODE+∠CDO=90°，
∴∠ODA=90°，
∴AB是⊙O的切线．           …（5分）
（Ⅱ）解：∵AB、BC是⊙O的切线，
∴OB⊥DC，
∴DE∥OB，∴∠CED=∠COB，
∵∠EDC=∠OCB，
∴△CDE∽△BCO，
∴

DE

CO

=

CE

BO

，
∴DE•OB=2R²=8，
∴⊙O的半径为2．…（10分）

点评：本题考查圆的切线，考查三角形相似的判断与运用，考查学生分析解决问题的能力，属于中档题．