题目内容
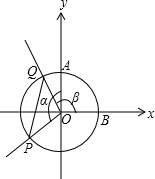
角α的顶点在坐标原点O,始边在y轴的正半轴上,终边与单位圆交于第三象限内的点P,且tanα=-
;角β的顶点在坐标原点O,始边在x轴的正半轴上,终边与单位圆交于第二象限内的点Q,且tanβ=-2.对于下列结论:
①P(-
,-
);
②|PQ|2=
;
③cos∠POQ=-
;
④△POQ的面积为
.
其中所有正确结论的序号有 .
| 3 |
| 4 |
①P(-
| 3 |
| 5 |
| 4 |
| 5 |
②|PQ|2=
10+2
| ||
| 5 |
③cos∠POQ=-
| 3 |
| 5 |
④△POQ的面积为
| ||
| 5 |
其中所有正确结论的序号有
考点:三角函数线
专题:三角函数的求值
分析:利用诱导公式得到OP所对应的角,结合平方关系求解
+α的正余弦值得答案,判断命题①;
求出Q的坐标,由两点间的距离公式计算|PQ|2,然后判断真假;
把两角差的余弦用诱导公式化为正弦,展开后计算得答案,再判断真假;
直接由面积公式求值,然后判断真假.
| π |
| 2 |
求出Q的坐标,由两点间的距离公式计算|PQ|2,然后判断真假;
把两角差的余弦用诱导公式化为正弦,展开后计算得答案,再判断真假;
直接由面积公式求值,然后判断真假.
解答:
解:如图,
对于①,由tanα=-
,得cot(α+
)=
,
∴
=
.
又sin2(α+
)+cos2(α+
)=1,
且α+
∈(π,
),
解得:sin(α+
)=-
,cos(α+
)=-
.
设P(x,y),
∴x=cos(α+
)=-
,sin(α+
)=-
.
∴P(-
,-
).命题①正确;
对于②,由tanβ=-2,得
=-2,
又sin2β+cos2β=1,且β∈(
,π),
解得:cosβ=-
,sinβ=
.
∴Q(-
,
).
∴|PQ|2=(-
+
)2+(-
-
)2=
.命题②正确;
对于③,cos∠POQ=cos(
+α-β)=-sin(α-β)
=-sinαcosβ+cosαsinβ=-
×(-
)+(-
)×
=-
.命题③错误;
对于④,由③得:sin∠POQ=
,
∴S△POQ=
×1×1×
=
.命题④正确.
∴正确的命题是①②④.
故答案为:①②④.

对于①,由tanα=-
| 3 |
| 4 |
| π |
| 2 |
| 3 |
| 4 |
∴
cos(α+
| ||
sin(α+
|
| 3 |
| 4 |
又sin2(α+
| π |
| 2 |
| π |
| 2 |
且α+
| π |
| 2 |
| 3π |
| 2 |
解得:sin(α+
| π |
| 2 |
| 4 |
| 5 |
| π |
| 2 |
| 3 |
| 5 |
设P(x,y),
∴x=cos(α+
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| 4 |
| 5 |
∴P(-
| 3 |
| 5 |
| 4 |
| 5 |
对于②,由tanβ=-2,得
| sinβ |
| cosβ |
又sin2β+cos2β=1,且β∈(
| π |
| 2 |
解得:cosβ=-
| ||
| 5 |
2
| ||
| 5 |
∴Q(-
| ||
| 5 |
2
| ||
| 5 |
∴|PQ|2=(-
| 3 |
| 5 |
| ||
| 5 |
| 4 |
| 5 |
2
| ||
| 5 |
10+2
| ||
| 5 |
对于③,cos∠POQ=cos(
| π |
| 2 |
=-sinαcosβ+cosαsinβ=-
| 3 |
| 5 |
| ||
| 5 |
| 4 |
| 5 |
2
| ||
| 5 |
| ||
| 5 |
对于④,由③得:sin∠POQ=
2
| ||
| 5 |
∴S△POQ=
| 1 |
| 2 |
2
| ||
| 5 |
| ||
| 5 |
∴正确的命题是①②④.
故答案为:①②④.
点评:本题考查命题的真假判断与应用,考查了三角函数线,训练了三角函数的诱导公式及同角三角函数基本关系式的用法,是中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
从区间[-5,5]内随机取出一个数x,从区间[-3,3]内随机取出一个数y,则使得|x|+|y|≤4的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
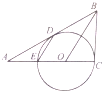 如图,以Rt△ABC直角边AC上一点O为圆心,OC为半径的⊙O与AC另一个交点E,D为斜边AB上一点且在⊙O上,AD2=AE•AC.
如图,以Rt△ABC直角边AC上一点O为圆心,OC为半径的⊙O与AC另一个交点E,D为斜边AB上一点且在⊙O上,AD2=AE•AC.