题目内容
某商店商品每件成本10元，若售价为25元，则每天能卖出288件，经调查，如果降低价格，销售量可以增加，且每天多卖出的商品件数t与商品单价的降低值x（单位：元，0≤x≤15）的关系是t=6x2．
（1）将每天的商品销售利润y表示成x的函数；
（2）如何定价才能使每天的商品销售利润最大？
（1）将每天的商品销售利润y表示成x的函数；
（2）如何定价才能使每天的商品销售利润最大？
考点：导数在最大值、最小值问题中的应用
专题：导数的综合应用
分析：（1）根据题意列出函数关系式即可；
（2）利用导数求函数的最大值即可解决．
（2）利用导数求函数的最大值即可解决．
解答：
解：（1）设商品降价x元，记商品每天的获利为f（x），则依题意得
f（x）=（25-10-x）（288+6x2）=（15-x）（288+6x2）=-6x3+90x2-288x+4320（0≤x≤15）----------（6分）
（2）根据（1），有f′（x）=-18x2+180x-288=-18（x-2）（x-8）．
当x变化时，f′（x）与f（x）的变化如下表：
故x=8时，f（x）取得极大值．因为f（8）=4704，f（0）=4320，
所以定价为25-8=17元能使一天的商品销售利润最大．----------（12分）
f（x）=（25-10-x）（288+6x2）=（15-x）（288+6x2）=-6x3+90x2-288x+4320（0≤x≤15）----------（6分）
（2）根据（1），有f′（x）=-18x2+180x-288=-18（x-2）（x-8）．
当x变化时，f′（x）与f（x）的变化如下表：
| x | [0，2） | 2 | （2，8） | 8 | （8，15] |
| f′（x） | - | 0 | + | 0 | - |
| f（x） | 单调递减 | 极小 | 单调递增 | 极大 | 单调递减 |
所以定价为25-8=17元能使一天的商品销售利润最大．----------（12分）
点评：本题主要考查导数在实际问题中的应用，考查利用导数求函数的最值问题，属中档题．
练习册系列答案
相关题目
在△ABC中，若a=2，b+c=7，cosB=-
，则b=（ ）
| 1 |
| 4 |
| A、3 | B、4 | C、5 | D、6 |
如图所示，一条直角走廊宽为a米．现有一转动灵活的平板车，其平板面为矩形，它的宽为b（0＜b＜a）米．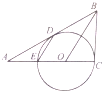
如图，以Rt△ABC直角边AC上一点O为圆心，OC为半径的⊙O与AC另一个交点E，D为斜边AB上一点且在⊙O上，AD2=AE•AC．