题目内容
已知E为不等式组
,表示区域内的一点,过点E的直线l与圆M:(x-1)2+y2=9相交于A,C两点,过点E与l垂直的直线交圆M于B、D两点,当AC取最小值时,四边形ABCD的面积为( )
|
A、4
| ||
B、6
| ||
C、12
| ||
| D、12 |
考点:简单线性规划
专题:数形结合
分析:由约束条件作出可行域,由圆的方程画出圆,可知可行域内距离圆心最远的点为满足条件的E点,求出E与M的距离,解直角三角形求得AC的长度,则四边形ABCD的面积为AC长度与BD长度乘积的一半.
解答:
解:由约束条件
作可行域如图,
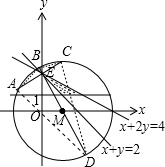
圆M:(x-1)2+y2=9的圆心为M(1,0),半径为3.
E为图中阴影三角形及其内部一动点,
由图可知,当E点位于直线x+y=2与y轴交点时,E为可行域内距离圆心M最远的点.
此时当AC过E且与ME垂直时最短.与AC垂直的直线交圆得到直径BD.
|ME|=
,|AC|=2
=4,
S四边形ABCD=
×6×4=12.
故选:D.
|

圆M:(x-1)2+y2=9的圆心为M(1,0),半径为3.
E为图中阴影三角形及其内部一动点,
由图可知,当E点位于直线x+y=2与y轴交点时,E为可行域内距离圆心M最远的点.
此时当AC过E且与ME垂直时最短.与AC垂直的直线交圆得到直径BD.
|ME|=
| 5 |
32-(
|
S四边形ABCD=
| 1 |
| 2 |
故选:D.
点评:本题考查简单的线性规划,考查数形结合的解题思想方法,关键是确定使AC最短时的E的位置,是中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知全集U=R,集合A={0,1,2,3,4,5},B={x∈R|x≥2},则A∩(∁UB)=( )
| A、{0,1} |
| B、{1} |
| C、{1,2} |
| D、{0,1,2} |
已知集合A={x|y=ln(3-x)},B={x|x2-5x+4≤0},则A∩B=( )
| A、{x|1≤x<3} |
| B、{x|1<x<3} |
| C、{x|0<x<4} |
| D、{x|0≤x≤4} |
在△ABC中,若a=2,b+c=7,cosB=-
,则b=( )
| 1 |
| 4 |
| A、3 | B、4 | C、5 | D、6 |
设a,b是关于x的方程x2sinθ+xcosθ-2=0(θ∈R)的两个互异实根,直线l过点A(a,a2),B(b,b2),则坐标原点O到直线l的距离是( )
| A、2 |
| B、2|tanθ| |
| C、2|cotθ| |
| D、2|sinθcosθ| |
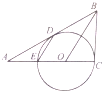 如图,以Rt△ABC直角边AC上一点O为圆心,OC为半径的⊙O与AC另一个交点E,D为斜边AB上一点且在⊙O上,AD2=AE•AC.
如图,以Rt△ABC直角边AC上一点O为圆心,OC为半径的⊙O与AC另一个交点E,D为斜边AB上一点且在⊙O上,AD2=AE•AC.