题目内容
14.已知函数f(x)=|x-a|+|2x-a|(a∈R).(1)若f(1)<11,求a的取值范围;
(2)若?a∈R,f(x)≥x2-x-3恒成立,求x的取值范围.
分析 (1)讨论a的范围,得出f(1)关于a的解析式,从而解出a的值;
(2)把a看作自变量,利用绝对值三角不等式得出|x-a|+|2x-a|的最小值,从而得出关于x的不等式解出.
解答 解:(1)f(1)=|1-a|+|2-a|=$\left\{\begin{array}{l}{3-2a,a≤1}\\{1,1<a<2}\\{2a-3,a≥2}\end{array}\right.$,
当a≤1时,3-2a<11,解得a>-4,∴-4<a≤1;
当1<a<2时,1<11恒成立;
当a≥2时,2a-3<11,解得a<4,2≤a<4.
综上,a的取值范围是(-4,4).
(2)f(x)=|x-a|+|2x-a|≥|x-a-(2x-a)|=|x|,
∴|x|≥x2-x-3,
∴$\left\{\begin{array}{l}{x≥{x}^{2}-x-3}\\{x≥0}\end{array}\right.$或$\left\{\begin{array}{l}{-x≥{x}^{2}-x-3}\\{x<0}\end{array}\right.$,
解得0≤x≤$\frac{1+\sqrt{13}}{2}$或-$\sqrt{3}≤$x<0.
∴-$\sqrt{3}$≤x≤$\frac{1+\sqrt{13}}{2}$.
点评 本题考查了绝对值不等式的解法,绝对值三角不等式,属于中档题.

练习册系列答案
相关题目
4.执行如图2所示的程序框图,若输出S=7,则输入k(k∈N*)的值为( )

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.下列函数为奇函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=|sinx| | C. | y=ex-e-x | D. | y=cosx |
6.若点A($\sqrt{3}$,1)的直线l1:$\sqrt{3}$x+ay-2=0与过点B($\sqrt{3}$,4)的直线l2交于点C,若△ABC是以AB为底边的等腰三角形,则l2的方程为( )
| A. | $\sqrt{3}$x+y-7=0 | B. | $\sqrt{3}$x-y+7=0 | C. | x+$\sqrt{3}$y-7=0 | D. | x-$\sqrt{3}$y-7=0 |
4.要得到函数y=sin(2x+$\frac{π}{3}$)的图象,只需将函数y=cos2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
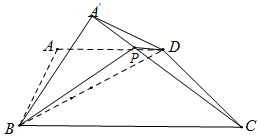 如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.