题目内容
已知直线y=kx-1与圆x2+y2+kx+my-4=0的交点M,N关于直线x+y=0对称,则m+k= .
考点:直线与圆相交的性质
专题:直线与圆
分析:由题意,得直线x+y=0是线段MN的中垂线,利用垂直直线的斜率关系算出k=1,得出圆方程为x2+y2+x+my-4=0,将圆心坐标代入x+y=0,解得m=2,可得本题答案.
解答:
解:∵直线y=kx-1与圆x2+y2+kx+my-4=0交于M,N两点,且M,N关于直线x+y=0对称,
∴直线x+y=0是线段MN的中垂线,得k•(-1)=-1,解之得k=1.
所以圆方程为x2+y2+x+my-4=0,圆心坐标为(-1,
),
将(-1,
)代入x+y=0,解得m=2,得k+m=3.
故答案为:3.
∴直线x+y=0是线段MN的中垂线,得k•(-1)=-1,解之得k=1.
所以圆方程为x2+y2+x+my-4=0,圆心坐标为(-1,
| m |
| 2 |
将(-1,
| m |
| 2 |
故答案为:3.
点评:本题给出直线与圆相交,且两个交点关于已知直线对称,求参数k、m的值.着重考查了直线的斜率、圆的方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法不正确的是( )
| A、函数关系是一种确定性关系 |
| B、相关关系是一种非确定性关系 |
| C、回归分析是对具有函数关系的两个变量进行统计分析的一种方法 |
| D、回归分析是对具有相关关系的两个变量进行统计分析的一种方法 |
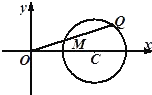 (理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.
(理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.