题目内容
设集合M={(x,y)|x2+y2≤4},N={(x,y)|(x-1)2+(y-1)2≤r2},(r>0),当M∩N=M,则r的最小值为 .
考点:交集及其运算
专题:集合
分析:集合M表示圆心为原点,半径为2的圆上及圆内的点,N表示圆心为(1,1),半径为r的圆上及圆内的点,根据M与N交集为M,得到M为N的子集,即可确定出r的范围.
解答:
 解:集合M表示圆心为(0,0),半径为2的圆上及圆内的点集;
解:集合M表示圆心为(0,0),半径为2的圆上及圆内的点集;
集合N表示圆心为(1,1),半径为r的圆上及圆内的点集,
∵M∩N=M,∴M⊆N,
则当两圆内切时,r最小,此时r=AB=OB+OA=2+
=2+
.
故答案为:2+
 解:集合M表示圆心为(0,0),半径为2的圆上及圆内的点集;
解:集合M表示圆心为(0,0),半径为2的圆上及圆内的点集;集合N表示圆心为(1,1),半径为r的圆上及圆内的点集,
∵M∩N=M,∴M⊆N,
则当两圆内切时,r最小,此时r=AB=OB+OA=2+
| 12+12 |
| 2 |
故答案为:2+
| 2 |
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,下列说法错误的是( )
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,下列说法错误的是( )| A、乙班平均身高高于甲班 | ||
| B、甲班的样本方差为57.2 | ||
C、从乙班这10名同学中随机抽取两名身高不低于173cm的同学,可得身高为176cm的同学被抽中的概率为
| ||
| D、乙班的中位数为178 |
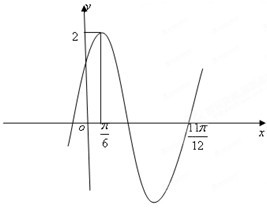 已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<
已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<