题目内容
8.2017年将进行高考改革,语文学科要加强对中华民族优秀传统文化的考查,充分体现语文的基础性和作为母语学科的重要地位,一时间“语文分值将会提高到180分”引起广泛关注,为了解在校大学生及社会人士(包括老师、家长等)的看法,某媒体在全省选择了3600人进行调查,就是否“提高语文分值”的问题,调查统计的结果如表:| 态度 调查人群 | 应该取消 | 不应该提高 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 600人 | x人 | z人 |
(1)求应在持“不应该提高”态度的人中抽取多少人?
(2)在持“不应该提高”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
分析 (1)先求出持“无所谓”态度的人数,由此能求出x,从而能求出持“不应该提高”态度的人数,进而由分层抽样的性质能求出应在持“不应该提高”态度的人中抽取的人数.
(2)在持“不应该提高”态度的人中,用分层抽样的方法抽取6人,在所抽取的6人中,在校学生人数为4人,社会人士为2人,第一组中在校学生人数ξ的可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(1)∵在全体样品中用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,其中持“无所谓”态度的人中抽取了72人,
∴持“无所谓”态度的人数为$\frac{3600}{360}×72$=720,
∴x=3600-2100-120-720=60,
∴持“不应该提高”态度的人数为:120+60=180人,
由分层抽样的性质得应在持“不应该提高”态度的人中抽取:180×$\frac{360}{3600}$=18人.
(2)在持“不应该提高”态度的人中,用分层抽样的方法抽取6人,
∴在所抽取的6人中,在校学生人数为$\frac{120}{180}×6=4$人,社会人士为:$\frac{60}{180}×6=2$人,
第一组中在校学生人数ξ的可能取值为1,2,3,
P(ξ=1)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(ξ=2)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(ξ=3)=$\frac{{C}_{4}^{3}{C}_{2}^{0}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查分层抽样的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

| A. | {x|x$≥-\sqrt{2}$} | B. | {x|-$\sqrt{2}$≤x≤-1} | C. | {x|-$\sqrt{2}≤x≤\sqrt{2}$} | D. | {x|-1$≤x≤\sqrt{2}$} |
| A. | (1,3) | B. | (1,2] | C. | $(\frac{1}{2},\frac{7}{2})$ | D. | 以上均不正确 |
| 得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 甲 | 5 | 10 | 34 | 11 |
| 乙 | 8 | 12 | 31 | 9 |
(Ⅱ)生产一件产品甲,若是合格品可盈利100元,若是不合格品则亏损20元;生产一件产品乙,若是合格品可盈利90元,若是不合格品则亏损15元.在(Ⅰ)的前提下:
(1)记X为生产1件甲和1件乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件乙所获得的利润不少于300元的概率.
| A. | 4+$\sqrt{2}$ | B. | 4-$\sqrt{2}$ | C. | 4 | D. | 5 |
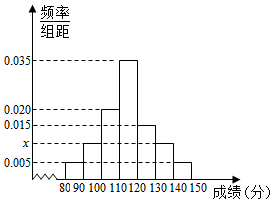 40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图:
40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图: