题目内容

17．某工厂有两条相互不影响的生产线分别生产甲、乙两种产品，产品出厂前需要对产品进行性能检测．检测得分低于80的为不合格品，只能报废回收；得分不低于80的为合格品，可以出厂．现随机抽取这两种产品各60件进行检测，检测结果统计如表：
得分[60，70）[70，80）[80，90）[90，100]
甲5103411
乙812319
（Ⅰ）试分别估计产品甲，乙下生产线时为合格品的概率；
（Ⅱ）生产一件产品甲，若是合格品可盈利100元，若是不合格品则亏损20元；生产一件产品乙，若是合格品可盈利90元，若是不合格品则亏损15元．在（Ⅰ）的前提下：
（1）记X为生产1件甲和1件乙所得的总利润，求随机变量X的分布列和数学期望；
（2）求生产5件乙所获得的利润不少于300元的概率．

分析 （I）求解运用古典概率得出甲，乙下生产线时为合格品的概率，
（Ⅱ）（1）确定随机变量X的所有可能取值为190，85，70，-35．
求解P（X=190），P（X=85），P（X=70），P（X=-35），求解分布列，
（2）设生产5件乙所获得的利润不少于300，运用二项分布问题求解，

解答 解：（Ⅰ）甲为合格品的概率约为：$\frac{45}{60}$=$\frac{3}{4}$，
乙为合格品的概率约为：$\frac{40}{60}$=$\frac{2}{3}$；              …（2分）
（Ⅱ）（1）随机变量x的所有取值为190，85，70，-35，而且
P（X=190）=$\frac{3}{4}$×$\frac{2}{3}$=$\frac{1}{2}$，P（X=85）=$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{4}$，
P（X=70）=$\frac{1}{4}$×$\frac{2}{3}$=$\frac{1}{6}$，P（X=-35）=$\frac{1}{4}$×$\frac{1}{3}$=$\frac{1}{12}$；
所以随机变量X的分布列为：

X1908570-35
P$\frac{1}{2}$$\frac{1}{4}$$\frac{1}{6}$$\frac{1}{12}$
…（6分）
所以：EX=$\frac{190}{2}+\frac{85}{4}+\frac{70}{6}-\frac{35}{12}$=125，…（8分）
（2）设生产的5件乙中正品有n件，则次品有5-n件，
依题意，90n-15（5-n）≥300，解得：n≥$\frac{25}{7}$，取n=4或n=5，
设“生产5件元件乙所获得的利润不少于300元”为事件A，则：
P（A）=C54（$\frac{2}{3}$）4$•\frac{1}{3}$+（$\frac{2}{3}$）5=$\frac{112}{243}$                   …（12分）

点评 本题考查了离散型的概率分布问题，确定随机变量的取值，关键是确定事件得出相应的概率，分清题意．

练习册系列答案
相关题目
7．一个算法的流程图如图所示，若输入x的值为1，则输出y的值是（　　）
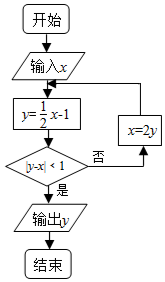
A．0B．-1C．-$\frac{3}{2}$D．-3
8．2017年将进行高考改革，语文学科要加强对中华民族优秀传统文化的考查，充分体现语文的基础性和作为母语学科的重要地位，一时间“语文分值将会提高到180分”引起广泛关注，为了解在校大学生及社会人士（包括老师、家长等）的看法，某媒体在全省选择了3600人进行调查，就是否“提高语文分值”的问题，调查统计的结果如表：
态度
调查人群		应该取消不应该提高无所谓
在校学生2100人120人y人
社会人士600人x人z人
媒体在全体样品中用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，其中持“无所谓”态度的人中抽取了72人．
（1）求应在持“不应该提高”态度的人中抽取多少人？
（2）在持“不应该提高”态度的人中，用分层抽样的方法抽取6人平均分成两组进行深入交流，求第一组中在校学生人数ξ的分布列和数学期望．
5．如图所示，当输入a，b分别为2，3时，最后输出的M的值是（　　）
A．1B．2C．3D．4
12．已知实数x，y满足$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+2y≤2}\end{array}\right.$，若目标函数z=x-y的最大值为a，最小值为b，则a+b=1．
2．设集合M={x|x2=x}，N={x|log2x≤0}，则M∪N=[0，1]．
9．已知点列An（an，bn）（n∈N*）均为函数y=ax（a＞0，a≠1）的图象上，点列Bn（n，0）满足|AnBn|=|AnBn+1|，若数列{bn}中任意连续三项能构成三角形的三边，则a的取值范围为（　　）
A．（0，$\frac{\sqrt{5}-1}{2}$）∪（$\frac{\sqrt{5}+1}{2}$，+∞）B．（$\frac{\sqrt{5}-1}{2}$，1）∪（1，$\frac{\sqrt{5}+1}{2}$）C．（0，$\frac{\sqrt{3}-1}{2}$）∪（$\frac{\sqrt{3}+1}{2}$，+∞）D．（$\frac{\sqrt{3}-1}{2}$，1）∪（1，$\frac{\sqrt{3}+1}{2}$）
6．如果0＜a＜b＜1，P=log${\;}_{0.5}\frac{a+b}{2}$，Q=$\frac{1}{2}$（log0.5a+log0.5b），M=$\frac{1}{2}$log0.5（a+b），那么P，Q，M的大小顺序是（　　）
A．P＞Q＞MB．Q＞P＞MC．Q＞M＞PD．M＞Q＞P
7．已知函数f（x）=sin（2x+φ）0＜φ＜$\frac{π}{2}$）的图象的一个对称中心为（$\frac{3π}{8}$，0），则函数f（x）的单调递减区间是（　　）
A．[2kπ-$\frac{3π}{8}$，2kπ+$\frac{π}{8}$]（k∈Z）B．[2kπ+$\frac{π}{8}$，2kπ+$\frac{5π}{8}$]（k∈Z）
C．[kπ-$\frac{3π}{8}$，kπ+$\frac{π}{8}$]（k∈Z）D．[kπ+$\frac{π}{8}$，kπ+$\frac{5π}{8}$]（k∈Z）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网