题目内容
19.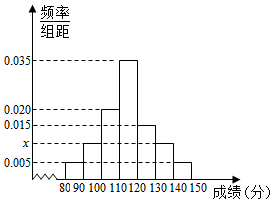 40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图:
40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如图:(Ⅰ)求频率分布直方图中x的值;
(Ⅱ)分别求出成绩落在(130,140]与(140,150]中的学生人数;
(Ⅲ)从成绩落在(130,150]中的学生中任选2人,求此2人中至少有1人的成绩落在(140,150]中的概率.
分析 (Ⅰ)根据频率和为1,列出方程,求出x的值;
(Ⅱ)根据频率=$\frac{频数}{样本容量}$,即可求出.
(Ⅲ)由(Ⅱ)知,成绩落在(130,150]的学生共有6人.
记成绩落在(130,140]中的4人为A1,A2,A3,A4,成绩落在(140,150]中的2人为B1,B2,则从成绩在(130,150]的6名学生任选2人的基本事件共有15个,根据概率公式计算即可.
解答 解:(Ⅰ)由频率分布直方图知组距=10,且(0.005+x+0.020+0.035+0.015+x+0.005)×10=1,
解得x=0.010. …(2分)
(Ⅱ)由条件及(Ⅰ)得:
成绩落在(130,140]中的学生人数为0.010×10×40=4,…(4分)
成绩落在(140,150]中的学生人数为0.005×10×40=2. …(6分)
(Ⅲ)由(Ⅱ)知,成绩落在(130,150]的学生共有6人.
记成绩落在(130,140]中的4人为A1,A2,A3,A4,成绩落在(140,150]中的2人为B1,B2,则从成绩在(130,150]的6名学生任选2人的基本事件共有15个:…(8分)(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)…(10分)
其中,选出的2人中至少有1人的成绩落在(140,150]中的基本事件有9个:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)
∴选出的2人中至少有1人的成绩落在(140,150]中的概率为$p=\frac{9}{15}=\frac{3}{5}$.…(12分)
点评 本题考查了频率分布直方图的应用问题,也考查了概率的计算,是基础题目.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案| A. | 5项 | B. | 6项 | C. | 7项 | D. | 8项 |
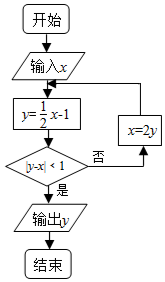
| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -3 |
| A. | (24,25) | B. | [16,25) | C. | (1,25) | D. | (0,25] |
| A. | 25 | B. | 35 | C. | 45 | D. | 55 |
| 态度 调查人群 | 应该取消 | 不应该提高 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 600人 | x人 | z人 |
(1)求应在持“不应该提高”态度的人中抽取多少人?
(2)在持“不应该提高”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
| A. | (0,$\frac{\sqrt{5}-1}{2}$)∪($\frac{\sqrt{5}+1}{2}$,+∞) | B. | ($\frac{\sqrt{5}-1}{2}$,1)∪(1,$\frac{\sqrt{5}+1}{2}$) | C. | (0,$\frac{\sqrt{3}-1}{2}$)∪($\frac{\sqrt{3}+1}{2}$,+∞) | D. | ($\frac{\sqrt{3}-1}{2}$,1)∪(1,$\frac{\sqrt{3}+1}{2}$) |