题目内容
已知二次函数f(x)=ax2+(4a-1)x+3a在区间[-
,3]上的最大值为3,求实数a的取值.
| 1 |
| 2 |
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:二次函数在闭区间上取得最大值的情况有:在端点处,在顶点处,所以分别让区间[-
,3]端点和顶点处取得最大值,求出对应的a,然后验证是否符合条件即可.
| 1 |
| 2 |
解答:
解:根据二次函数在端点处或顶点取得最大值得:
(1)若f(-
)=3,即
-
+3a=3,解得a=2;
∴f(x)=2x2+7x+6=2(x+
)2-
,∴f(3)是最大值,所以这种情况不存在;
(2)若f(3)=3,即9a+12a-3+3a=3,解得a=
;
∴f(x)=
+
,∴;f(3)f(3)是最大值,且f(3)=3,所以这种情况正确;
(3)若f(
)=3,即
+(4a-1)•
+3a=3,解a=-
;
∴f(x)=-
x2-3x-
=-
(x+3)2+3,所以f(-
)最大,所以这种情况不存在;
综上得a=
.
(1)若f(-
| 1 |
| 2 |
| a |
| 4 |
| 4a-1 |
| 2 |
∴f(x)=2x2+7x+6=2(x+
| 7 |
| 4 |
| 1 |
| 8 |
(2)若f(3)=3,即9a+12a-3+3a=3,解得a=
| 1 |
| 4 |
∴f(x)=
| x2 |
| 4 |
| 3 |
| 4 |
(3)若f(
| 1-4a |
| 2a |
| (1-4a)2 |
| 4a |
| 1-4a |
| 2a |
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上得a=
| 1 |
| 4 |
点评:考查二次函数在闭区间上取得最大值的可能情况,配方法求二次函数的最大值.

练习册系列答案
相关题目
数列{an}中,a2=2,a6=0且数列{
}是等差数列,则a8=( )
| 1 |
| an+1 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
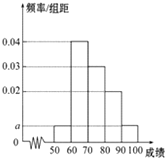 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]