题目内容
不用计算器,求值:tan10°tan20°tan30°tan40°tan50°tan60°tan70°tan80°.
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:根据一个角的正切等它于余角的余切,根据同角的正切与余切的积是1,可得答案.
解答:
解:∵tanα=cot(90°-α).
∴原式=cot80°•cot70°•cot60°•cot50°•tan50°•tan60°•tan70°•tan80°
=1.
故答案为:1.
∴原式=cot80°•cot70°•cot60°•cot50°•tan50°•tan60°•tan70°•tan80°
=1.
故答案为:1.
点评:本题考查了互余两角三角函数的关系,利用了一个角的正切等它于余角的余切,同角的正切与余切的积是1.

练习册系列答案
相关题目
若函数y=f(2x+1)的定义域为[-1,2],则g(x)=f(x)+f(-x)的定义域是( )
| A、[-1,1] |
| B、[-5,5] |
| C、[-1,5] |
| D、[-5,1] |
不等式x2-x-6<0解集为( )
| A、{x|-2<x<3} |
| B、{x|-3<x<2} |
| C、{x|x<-3或x>2} |
| D、{x|-1<x<6} |
设m,n∈R+,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的最小值是( )
A、2+
| ||
B、2+2
| ||
C、4-
| ||
D、4-2
|
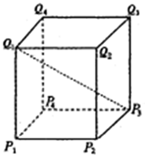 若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,集合M={x|x=
若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,集合M={x|x=