题目内容
已知sinθ-cosθ=
,则sin2θ-cos2θ= .
| 1 |
| 2 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:由条件求得sin2θ=
,再根据sin2θ-cos2θ=-cos2θ=±
,计算求得结果.
| 3 |
| 4 |
| 1-sin22θ |
解答:
解:∵已知sinθ-cosθ=
,∴1-sin2θ=
,∴sin2θ=
,
∴sin2θ-cos2θ=-cos2θ=±
=±
,
故答案为:±
.
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
∴sin2θ-cos2θ=-cos2θ=±
| 1-sin22θ |
| ||
| 4 |
故答案为:±
| ||
| 4 |
点评:本题主要考查同角三角函数的基本关系、二倍角的公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知点O为坐标原点,点A(1,0,0)、点B(1,1,0),则下列各向量中是平面AOB的一个法向量的是( )
| A、(1,1,1) |
| B、(1,0,1) |
| C、(0,1,1) |
| D、(0,0,1) |
若函数y=f(2x+1)的定义域为[-1,2],则g(x)=f(x)+f(-x)的定义域是( )
| A、[-1,1] |
| B、[-5,5] |
| C、[-1,5] |
| D、[-5,1] |
设扇形的周长为8cm,面积为4cm2,则扇形的圆心角是( )rad.
| A、1 | B、2 | C、π | D、1或2 |
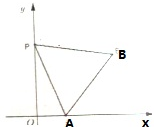 如图在平面内放置的边长为1的正三角形PAB沿x轴滚动,设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为
如图在平面内放置的边长为1的正三角形PAB沿x轴滚动,设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为