题目内容
与圆x2+y2-4x+3=0外切，与直线x=-1相切的动圆圆心的轨迹方程是 ．
考点：抛物线的定义
专题：圆锥曲线的定义、性质与方程
分析：圆x2+y2-4x+3=0化为（x-2）2+y2=1的圆心C（2，0），可得与圆x2+y2-4x+3=0外切，与直线x=-1相切的动圆圆心满足：到定点C（2，0）与到定直线x=-2的距离相等，利用抛物线的定义即可得出．
解答：
解：圆x2+y2-4x+3=0化为（x-2）2+y2=1的圆心C（2，0），
与圆x2+y2-4x+3=0外切，与直线x=-1相切的动圆圆心满足：到定点C（2，0）与到定直线x=-2的距离相等，
因此与圆x2+y2-4x+3=0外切，与直线x=-1相切的动圆圆心的轨迹是抛物线：y2=8x．
故答案为：y2=8x．
与圆x2+y2-4x+3=0外切，与直线x=-1相切的动圆圆心满足：到定点C（2，0）与到定直线x=-2的距离相等，
因此与圆x2+y2-4x+3=0外切，与直线x=-1相切的动圆圆心的轨迹是抛物线：y2=8x．
故答案为：y2=8x．
点评：本题考查了圆与圆外切及圆与直线相切性质、抛物线的定义，考查了推理能力，属于基础题．
练习册系列答案
相关题目
根据如图所示的框图，对大于2的整数N，输出的数列的通项公式是（ ）
| A、an=2n-1 |
| B、an=2n |
| C、an=2（n-1） |
| D、an=2n |
既是周期为π的偶函数又在区间(0，
)上单调递减的函数是（ ）
| π |
| 2 |
| A、y=sinx |
| B、y=cosx |
| C、y=sin2x |
| D、y=cos2x |
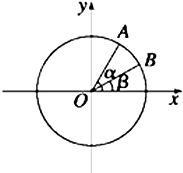（1）已知cos（