Question

（1）已知cos（

π

6

-α）=

3

3

，求cos（

5π

6

+α）-sin²（α-

π

6

）的值．
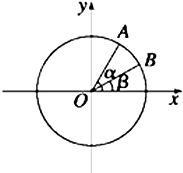
（2）如图，在平面直角坐标系xoy中，以x轴为始边作两个锐角α，β，它们的终边分别与单位圆交于A，B两点．已知A，B的横坐标分别为

5

5

，

7 2

10

．求tanα，tanβ的值．

Answer 1

考点：三角函数的化简求值,单位圆与周期性

专题：计算题,三角函数的求值

分析：（1）由角的关系可知原式=-cos（

π

6

-α）-1+cos²（

π

6

-α）代入已知即可求值．
（2）先求得sinα=

5

5

，sinβ=

7 2

10

，α，β是两个锐角，故有cosα=

1-sin2α

=

2 5

5

，cosβ=

1-sin2β

=

2

10

，从而可求tanα，tanβ的值．

解答： 解：（1）∵cos（

π

6

-α）=

3

3

，
∴cos（

5π

6

+α）-sin²（α-

π

6

）=cos[π-（

π

6

-α）]-sin²（

π

6

-α）=-cos（

π

6

-α）-1+cos²（

π

6

-α）=-

2+ 3

3

．
（2）∵由已知可得sinα=

5

5

，sinβ=

7 2

10

，α，β是两个锐角
∴cosα=

1-sin2α

=

2 5

5

，cosβ=

1-sin2β

=

2

10

∴tanα=

1

2

，tanβ=7．

点评：本题主要考察了三角函数的化简求值，单位圆与周期性，属于基本知识的考查．