题目内容
点P(x,y)在以A(-3,1)、B(-1,0)、C(-2,0)为顶点的△ABC的内部运动(不包括边界),则
的取值范围是 .
| y-2 |
| x-1 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,设k=
,利用k的几何意义即可得到结论.
| y-2 |
| x-1 |
解答:
解:设k=
,则k的几何意义是P与定点D(1,2)连线的斜率,
作出可行域,由图象可知
则BD的斜率最大为
=1,AD的斜率最小为
=
,
故
<k<1,
故答案为:(
,1).
| y-2 |
| x-1 |
作出可行域,由图象可知

则BD的斜率最大为
| -2 |
| -1-1 |
| 1-2 |
| -3-1 |
| 1 |
| 4 |
故
| 1 |
| 4 |
故答案为:(
| 1 |
| 4 |
点评:本题主要考查线性规划的应用,利用数形结合以及直线的斜率公式是解决本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=
x3-2x2+3x+
,则与f(x)图象相切的斜率最小的切线方程为( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、2x-y-3=0 |
| B、x+y-3=0 |
| C、x-y-3=0 |
| D、2x+y-3=0 |
某战士在打靶中,连续射击两次,事件“至少有一次中靶”的对立事件是( )
| A、两次都不中 |
| B、至多有一次中靶 |
| C、两次都中靶 |
| D、只有一次中靶 |
设f(x)=x+ln(x+
),若对于任意的实数a和b,都有f(a)+f(b)>0,则必有( )
| 1+x2 |
| A、a+b>0 |
| B、a-b>0 |
| C、a+b<0 |
| D、a-b<0 |
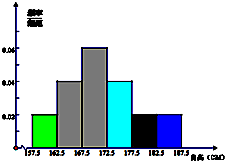 云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的平均身高为170.5cm.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],
云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的平均身高为170.5cm.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],