题目内容
若点M在直线a上，a在平面α内，则M，a，α间的上述关系的集合表示可记作（ ）
| A、M∈a∈α |
| B、M∈a⊆α |
| C、M⊆a⊆α |
| D、M⊆a∈α |
考点：空间中直线与平面之间的位置关系
专题：规律型,空间位置关系与距离
分析：点在直线上，称点属于直线，直线在平面内，称作直线真包含于平面，利用集合中元素与集合的关系符号、集合与集合的关系符号表达即得．
解答：
解：∵点M在直线a上，∴M∈a，
∵a在平面α内，∴a⊆α
∴M∈a⊆α，
故选：B．
∵a在平面α内，∴a⊆α
∴M∈a⊆α，
故选：B．
点评：本题考查点与直线、直线与平面的位置关系的表示，是基础题．
练习册系列答案
相关题目
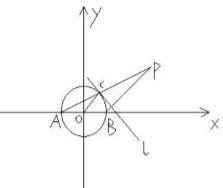已知A，B是⊙0：x2+y2=4与x轴的两个交点，C是⊙O上异于点A，B的任意一点，过点B作直线l的垂线BP，且与AC的延长线交于点P，求点P的轨迹方程．
如图，E、F分别是三棱锥P-ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（ ）| A、30° | B、60° |
| C、0° | D、120° |
如果双曲线的a=2，一个焦点为（5，0），则其标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
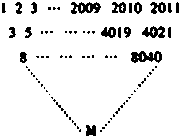给定三角形数表如图所示，其中第一行各数依次是1，2，3，…，2009，2010，2011，从第二行起，每个数分别等于它上面一行左、右两数之和，设第i行第j个数为f（i，j）（i，j∈N*，i+j≤2012），则：f（8，1）=设α，β，γ是三个互不重合的平面，m，n是两条不重合的直线，则下列命题中正确的是（ ）
| A、若m∥α，n∥β，α⊥β，则m⊥n |
| B、若α∥β，m?β，m∥α，则m∥β |
| C、若α⊥β，m⊥α，则m∥β |
| D、若α⊥β，β⊥γ，则α⊥γ |