Question

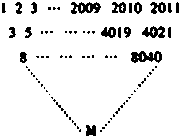给定三角形数表如图所示，其中第一行各数依次是1，2，3，…，2009，2010，2011，从第二行起，每个数分别等于它上面一行左、右两数之和，设第i行第j个数为f（i，j）（i，j∈N^*，i+j≤2012），则：f（8，1）=

 

，f（i，j）=

 

（用i和j表示）

Answer 1

考点：数列与函数的综合

专题：函数的性质及应用,等差数列与等比数列

分析：根据题意可知

f(n，1)

2n

=

f(n-1，1)

2n-1

+

1

4

，得出f（n，1）=（n+1）•2^n-2，
f（n，1）=f（n-1，1）+f（n-1，1）+2^n-2，运用求解即可．

解答： 解：∵f（n，1）=f（n-1，1）+f（n-1，2）=f（n-1，1）+f（n-1，1）+2^n-2=2f（n-1，1）+2^n-2
∴

f(n，1)

2n

=

f(n-1，1)

2n-1

+

1

4

∴

f(n，1)

2n

=

1

2

+

1

4

（n-1）=

n+1

4

∴f（n，1）=（n+1）•2^n-2
∴f（8，1）=9×2⁶=576，
∴f（i，1）=（i+1）•2^i-2，
f（i，j）=f（i，1）+（j-1）•2^i-1=（i+2j-1）•2^i-2．
故答案为：576；（i+2j-1）•2^i-2

点评：本题考查了数列的函数性质，运用递推的方法求解判断，属于很新颖的题目，中档题．