Question

6．如图，动点M与两定点A（-1，0），B（2，0）构成△MAB，且∠MBA=2∠MAB，求动点M的轨迹C的方程．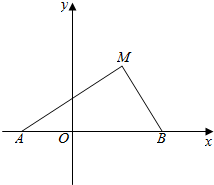

Answer 1

分析 设出点M（x，y），分类讨论，根据∠MBA=2∠MAB，利用正切函数公式，建立方程化简即可得到点M的轨迹方程．

解答 解：设M的坐标为（x，y），显然有x＞0，且y≠0
当∠MBA=90°时，点M的坐标为（2，±3）
当∠MBA≠90°时，x≠2，由∠MBA=2∠MAB有tan∠MBA=$\frac{2tan∠MAB}{1-ta{n}^{2}∠MAB}$，
化简可得3x²-y²-3=0
而点（2，±3）在曲线3x²-y²-3=0上
综上可知，轨迹C的方程为3x²-y²-3=0（x＞1）．

点评 本题以角的关系为载体，考查轨迹方程的求解，考查思维能力，运算能力，考查思维的严谨性，属于中档题．