题目内容
16．函数f（x）=x3+b$\root{3}{x}$+1（x∈R），若f（a）=2，则f（-a）的值为（ ）| A． | -3 | B． | 0 | C． | -1 | D． | -2 |
分析 由题意得f（x）-1=x3+b$\root{3}{x}$在R上是奇函数，从而可得f（-a）=0．
解答 解：∵函数f（x）=x3+b$\root{3}{x}$+1，
∴f（x）-1=x3+b$\root{3}{x}$在R上是奇函数，
∵f（a）-1=1，
∴f（-a）-1=-1，
∴f（-a）=0，
故选：B．
点评 本题考查了函数的奇偶性的判断与应用．
练习册系列答案
相关题目
6．数列{an}中an=$\frac{1}{{n}^{2}}$（n∈N*），f（n）=（1-a3）（1-a4）…（1-an），f（n）=（ ）
| A． | $\frac{2n+2}{{n}^{2}}$ | B． | $\frac{n+5}{3n}$ | C． | $\frac{2n+2}{3n}$ | D． | $\frac{2n+2}{2n+3}$ |
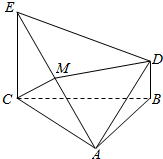如图，△ABC为正三角形，EC⊥平面ABC，BD∥CE，且CE=CA=2BD，M是EA的中点．