题目内容
下列命题正确的个数是( )
①若直线与平面有两个公共点,则直线在平面内;
②若直线l上有无数个点不在平面α内,则l∥α;
③若直线l与平面α相交,则直线l与平面α内的任意直线都是异面直线;
④若平面α∥平面β,直线a?α,直线b?β,则直线a∥b;
⑤若直线l与平面α不平行,则直线l与平面α有公共点;
⑥如果两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交.
①若直线与平面有两个公共点,则直线在平面内;
②若直线l上有无数个点不在平面α内,则l∥α;
③若直线l与平面α相交,则直线l与平面α内的任意直线都是异面直线;
④若平面α∥平面β,直线a?α,直线b?β,则直线a∥b;
⑤若直线l与平面α不平行,则直线l与平面α有公共点;
⑥如果两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①若直线与平面有两个公共点,
则由公理二知直线在平面内,故①正确;
②若直线l上有无数个点不在平面α内,则l与α相交或平行,故②错误;
③若直线l与平面α相交,
则直线l与平面α内的不过交点的直线都是异面直线,故③错误;
④若平面α∥平面β,直线a?α,直线b?β,则直线a与b平行或异面,故④错误;
⑤直线l与平面α不平行,则直线l与α相交或在面内,即l与α有一个或无穷多个公共点,故⑤正确;
⑥如果两条异面直线中的一条与一个平面平行,
则另一条直线一定与该平面相交、平行或者在平面内,故⑥错误.
故选:B.
则由公理二知直线在平面内,故①正确;
②若直线l上有无数个点不在平面α内,则l与α相交或平行,故②错误;
③若直线l与平面α相交,
则直线l与平面α内的不过交点的直线都是异面直线,故③错误;
④若平面α∥平面β,直线a?α,直线b?β,则直线a与b平行或异面,故④错误;
⑤直线l与平面α不平行,则直线l与α相交或在面内,即l与α有一个或无穷多个公共点,故⑤正确;
⑥如果两条异面直线中的一条与一个平面平行,
则另一条直线一定与该平面相交、平行或者在平面内,故⑥错误.
故选:B.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(
+
)n展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
| x |
| 2 |
| x2 |
| A、180 | B、90 |
| C、45 | D、360 |
在运行如图的程序框图时,若输入的x的值是-1,则输出y的值为( )


| A、-1 | B、0 | C、1 | D、2 |
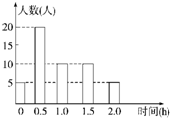 某校为了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天课外阅读所用时间的数据,结果用条形图表示如下.根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
某校为了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天课外阅读所用时间的数据,结果用条形图表示如下.根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )| A、0.6 h |
| B、0.9 h |
| C、1.0 h |
| D、1.5 h |
△ABC中,a=2,b=4,则∠A的取值范围是( )
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、(
|
已知函数f(x)=
,则函数y=f[f(x)]的零点个数是( )
|
| A、2 | B、3 | C、4 | D、6 |
下列各选项中,与sin2013°最接近的数是( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|