题目内容
函数f(x)是定义在区间[-5,5]上的偶函数,且在[0,5]上是单调函数,f(1)<f(3),则下列各式一定成立的是( )
| A、f(0)>f(5) |
| B、f(3)<f(2) |
| C、f(-1)>f(3) |
| D、f(-2)>f(1) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由于偶函数f(x)在[0,5]上是单调函数,且f(-3)<f(1)⇒f(x)在[0,5]上是单调递减,又f(-x)=f(x),从而可排除A、B、C,从而得到答案.
解答:
解:∵偶函数f(x)在[0,5]上是单调函数,且f(1)<f(3),
∴f(x)在[0,5]上是单调递增,在[-5,0)上是单调递减,
∴f(0)<f(5),f(3)>f(2),f(-1)=f(1)<f(3),f(-2)=f(2)>f(1),
故选:D.
∴f(x)在[0,5]上是单调递增,在[-5,0)上是单调递减,
∴f(0)<f(5),f(3)>f(2),f(-1)=f(1)<f(3),f(-2)=f(2)>f(1),
故选:D.
点评:本题考查奇偶性与单调性的综合,着重考查学生对函数奇偶性与单调性的理解与应用,特别注重排除法的应用,属于中档题.

练习册系列答案
相关题目
计算定积分
(x2+sinx)dx=( )
| ∫ | 1 -1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
(
+
)n展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
| x |
| 2 |
| x2 |
| A、180 | B、90 |
| C、45 | D、360 |
对于实数对(a,b)和(c,d),规定:(a,b)=(c,d)当且仅当a=c,c=d定义运算如下:
①(a,b)?(c,d)=(ac-bd,bc+ad);
②(a,b)⊕(c,d)=(a+c,b+d).
设p,q∈R,若(1,2)?(p,q)=(5,0),则(1,2)⊕(p,q)等于( )
①(a,b)?(c,d)=(ac-bd,bc+ad);
②(a,b)⊕(c,d)=(a+c,b+d).
设p,q∈R,若(1,2)?(p,q)=(5,0),则(1,2)⊕(p,q)等于( )
| A、(4,0) |
| B、(2,0) |
| C、(0,2) |
| D、(0,2) |
若函数f(x)是以
为周期的函数,且f(
)=1,则f(
π)=( )
| π |
| 2 |
| π |
| 3 |
| 17 |
| 6 |
| A、1 | B、2 | C、3 | D、4 |
已知{an}是等比数列,a2=2,a3=
,则公比q=( )
| 1 |
| 4 |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
在运行如图的程序框图时,若输入的x的值是-1,则输出y的值为( )


| A、-1 | B、0 | C、1 | D、2 |
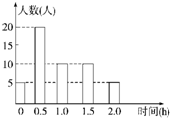 某校为了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天课外阅读所用时间的数据,结果用条形图表示如下.根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
某校为了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天课外阅读所用时间的数据,结果用条形图表示如下.根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )| A、0.6 h |
| B、0.9 h |
| C、1.0 h |
| D、1.5 h |