题目内容
19.狄利克雷函数是高等数学中的一个典型函数,若f(x)=$\left\{\begin{array}{l}{1,x∈Q}\\{0,x∈{C}_{R}Q}\end{array}\right.$,则称f(x)为狄利克雷函数.对于狄利克雷函数f(x),给出下面4个命题:①对任意x∈R,都有f[f(x)]=1;②对任意x∈R,都有f(-x)+f(x)=0;③对任意x1∈R,都有x2∈Q,f(x1+x2 )=f(x1);④对任意a,b∈(-∞,0),都有{x|f(x)>a}={x|f(x)>b}.其中所有真命题的序号是( )| A. | ①④ | B. | ③④ | C. | ①②③ | D. | ①③④ |
分析 根据狄利克雷函数,分别讨论当x∈Q和x∈∁RQ时,对应命题是否成立即可.
解答 解:①当x∈Q,则f(x)=1,f(1)=1,则[f(x)]=1,
当x∈∁RQ,则f(x)=0,f(0)=1,则[f(x)]=1,即对任意x∈R,都有f[f(x)]=1,故①正确,
②当x∈Q,则-x∈Q,则f(-x)=1,f(x)=1,此时f(-x)=f(x),
当x∈∁RQ,则-x∈∁RQ,则f(-x)=0,f(x)=0,此时f(-x)=f(x),
即恒有f(-x)=f(x),即函数f(x)是偶函数,故②错误,
③当x1∈Q,有x2∈Q,则x1+x2∈Q,此时f(x1+x2 )=f(x1)=1;
当x1∈∁RQ,有x2∈Q,则x1+x2∈∁RQ,此时f(x1+x2 )=f(x1)=0;
综上恒有f(x1+x2 )=f(x1)成立,故③正确,
④∵f(x)≥0恒成立,∴对任意a,b∈(-∞,0),都有{x|f(x)>a}={x|f(x)>b}=R,故④正确,
故正确的命题是①③④,
故选:D
点评 本题主要考查命题的真假判断,涉及新定义,正确理解狄利克雷函数的分段函数意义是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若在甲袋内装有8个白球,4个红球,在乙袋内装有6个白球,6个红球,今从两袋里任意取出1个球,设取出的白球个数为ξ,则下列概率中等于$\frac{{C}_{8}^{1}{C}_{6}^{1}+{C}_{4}^{1}{C}_{6}^{1}}{{C}_{12}^{1}{C}_{12}^{1}}$ 的是( )
| A. | P(ξ=0) | B. | P(ξ≤2) | C. | P(ξ=1) | D. | P(ξ=2) |
14.若复数z满足(1+2i)z=1-i,则复数z的虚部为( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$i | D. | -$\frac{3}{5}$i |
8.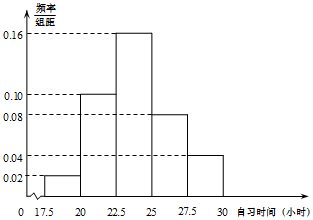 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )| A. | 30 | B. | 60 | C. | 80 | D. | 120 |
9.设等差数列{an}的前n项和为Sn,若a4,a6是方程x2-18x+p=0的两根,那么S9=( )
| A. | 9 | B. | 81 | C. | 5 | D. | 45 |