题目内容
8.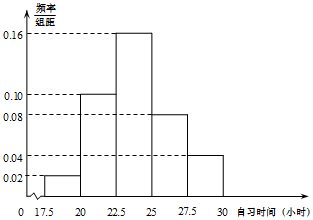 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )| A. | 30 | B. | 60 | C. | 80 | D. | 120 |
分析 根据已知中的频率分布直方图,先计算出自习时间不低于25小时的频率,进而可得自习时间不低于25小时的频数.
解答 解:自习时间不低于25小时的频率为:(0.08+0.04)×2.5=0.3,
故自习时间不低于25小时的频率为:0.3×200=60,
故选:B
点评 本题考查的知识点是频率分布直方图,难度不大,属于基础题目.

练习册系列答案
相关题目
18.已知$\left\{{\sqrt{a_n}}\right\}$是等比数列,a1=1,a2=2,则{an}的前5项和为( )
| A. | 31 | B. | 30 | C. | $31\sqrt{2}$ | D. | $30\sqrt{2}$ |
3.若函数f(x)=$\frac{1}{2}$x2-ax+lnx有极值,则a的取值范围是( )
| A. | (-∞,-2) | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (2,+∞) |
18.设曲线y=ex-x及直线y=0所围成的图形为区域D,不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$所确定的区域为E,在区域E内随机取一点,则该点落在区域D内的概率为( )
| A. | $\frac{{{e^2}-2e-1}}{4e}$ | B. | $\frac{{{e^2}-2e}}{4e}$ | C. | $\frac{{{e^2}-e-1}}{4e}$ | D. | $\frac{{{e^2}-1}}{4e}$ |
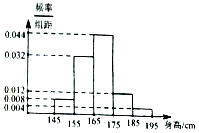 某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.
某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.