题目内容
已知函数f（x）=ex，如果x1，x2∈R，且x1≠x2，下列关于f（x）的性质，其中正确的是（ ）
①（x1-x2）[f（x1）-f（x2）]＞0；
②f（-x）=f（x）；
③f（-x）=-f（x）；
④
＞f（
）．
①（x1-x2）[f（x1）-f（x2）]＞0；
②f（-x）=f（x）；
③f（-x）=-f（x）；
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| A、①② | B、①③ | C、②④ | D、①④ |
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：利用函数的单调性判断①的正误；通过函数奇偶性判断②③的正误；利用函数的凹凸性判断④的正误；
解答：
解：函数f（x）=ex，函数是单调增函数，如果x1，x2∈R，且x1≠x2，
①（x1-x2）[f（x1）-f（x2）]＞0；说明函数是增函数，满足题意，∴①正确；
②③f（-x）=e-X≠ex=f（x），不存在奇偶性，∴②③不正确；
④具有性质的函数是凹函数，而f（x）=ex是凹函数；∴正确；
综上正确的结果为：①④．
故选：D．
①（x1-x2）[f（x1）-f（x2）]＞0；说明函数是增函数，满足题意，∴①正确；
②③f（-x）=e-X≠ex=f（x），不存在奇偶性，∴②③不正确；
④具有性质的函数是凹函数，而f（x）=ex是凹函数；∴正确；
综上正确的结果为：①④．
故选：D．
点评：本题考查函数的基本性质的应用，函数的单调性、反函数函数的凹凸性以及函数的零点，基本知识考查．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
在△ABC中，a=1，b=
，∠A=
，则∠B等于（ ）
| 3 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
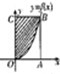如图，长方形四个顶点为O（0，0），A（