题目内容
已知函数f(x)=(x2-a+1)ex,g(x)=(x2-2)ex+2.
(1)若曲线y=f(x)在(1,f(1))处的切线为l:y=2ex+b,求a,b的值;
(2)若函数f(x)在[-3,1]上是单调函数,求实数a的取值范围;
(3)若f(x)有两个不同极值点m,n(m<n),且|m+n|≥|mn|-1,记F(x)=e2f(x)+g(x),求F(m)的最大值.
(1)若曲线y=f(x)在(1,f(1))处的切线为l:y=2ex+b,求a,b的值;
(2)若函数f(x)在[-3,1]上是单调函数,求实数a的取值范围;
(3)若f(x)有两个不同极值点m,n(m<n),且|m+n|≥|mn|-1,记F(x)=e2f(x)+g(x),求F(m)的最大值.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)根据导数的几何意义,即可求出切线的斜率,故求出a,b的值,
(2)需要分两种情况讨论,单调递增和单调递减,采用分离参数法,求出参数的最值即可,
(3)先求出a的范围,再求出m的范围,化简F(x),根据导数求出F(m)的最大值.
(2)需要分两种情况讨论,单调递增和单调递减,采用分离参数法,求出参数的最值即可,
(3)先求出a的范围,再求出m的范围,化简F(x),根据导数求出F(m)的最大值.
解答:
解:(1)f′(x)=(x2+2x-a+1)ex
由题意:f′(1)=(4-a)e=2e,
解得:a=2,
∴f(x)=(x2-1)ex
又f(1)=0=2e+b,
∴b=-2e
(2)若函数f(x)在[-3,1]上是单调递增函数
则f′(x)=(x2+2x-a+1)ex≥0在[-3,1]上恒成立,
即x2+2x-a+1≥0,
∴a≤x2+2x+1=(x+1)2在[-3,1]上恒成立,
∴a≤0,
若函数f(x)在[-3,1]上是单调递减函数
则f′(x)=(x2+2x-a+1)ex≤0在[-3,1]上恒成立,
即x2+2x-a+1≤0,
a≥x2+2x+1=(x+1)2在[-3,1]上恒成立,
∴a≥4,
综上,若函数f(x)在[-3,1]上是单调函数,则a的取值范围是(-∞,0]∪[4,+∞);
(3)令f′(x)=0得:x2+2x-a+1=0
由题意:△=4-4(1-a)=4a>0,
即a>0,
且:m+n=-2,mn=1-a(m<n),
∵|m+n|≥|mn|-1,
∴|a-1|≤3,
∴0<a≤4,
∵f′(m)=(m2+2m-a+1)em=0,
∴a=m2+2m+1,
∴0<m2+2m+1≤4
∴-3≤m≤1且m≠-1,
又∵m<n,
∴-3≤m<-1
∴F(x)=(x2-a+1)ex+2+(x2-2)ex+2=(2x2-a-1)ex+2
∴F(m)=(2m2-a-1)em+2=(m2-2m-2)em+2
∴F′(m)=(m2-4)em+2
∴F(m)在[-3,-2]上单调递增,在[-2,-1)上单调递减
∴Fmax(m)=F(-2)=6.
由题意:f′(1)=(4-a)e=2e,
解得:a=2,
∴f(x)=(x2-1)ex
又f(1)=0=2e+b,
∴b=-2e
(2)若函数f(x)在[-3,1]上是单调递增函数
则f′(x)=(x2+2x-a+1)ex≥0在[-3,1]上恒成立,
即x2+2x-a+1≥0,
∴a≤x2+2x+1=(x+1)2在[-3,1]上恒成立,
∴a≤0,
若函数f(x)在[-3,1]上是单调递减函数
则f′(x)=(x2+2x-a+1)ex≤0在[-3,1]上恒成立,
即x2+2x-a+1≤0,
a≥x2+2x+1=(x+1)2在[-3,1]上恒成立,
∴a≥4,
综上,若函数f(x)在[-3,1]上是单调函数,则a的取值范围是(-∞,0]∪[4,+∞);
(3)令f′(x)=0得:x2+2x-a+1=0
由题意:△=4-4(1-a)=4a>0,
即a>0,
且:m+n=-2,mn=1-a(m<n),
∵|m+n|≥|mn|-1,
∴|a-1|≤3,
∴0<a≤4,
∵f′(m)=(m2+2m-a+1)em=0,
∴a=m2+2m+1,
∴0<m2+2m+1≤4
∴-3≤m≤1且m≠-1,
又∵m<n,
∴-3≤m<-1
∴F(x)=(x2-a+1)ex+2+(x2-2)ex+2=(2x2-a-1)ex+2
∴F(m)=(2m2-a-1)em+2=(m2-2m-2)em+2
∴F′(m)=(m2-4)em+2
∴F(m)在[-3,-2]上单调递增,在[-2,-1)上单调递减
∴Fmax(m)=F(-2)=6.
点评:本题考查了利用导数研究函数在闭区间上的最值,一般是求出导函数对应方程的根,然后求出跟对应的函数值,区间端点的函数值,然后比较大小即可得到函数在闭区间上的最值.同时考查了利用导数研究函数的极值,求函数极值的步骤是:先求导函数,令导函数等于0,求出方程的根,确定函数在方程的根左右的单调性,根据极值的定义,确定极值点和极值.过程中要注意运用导数确定函数的单调性,一般导数的正负对应着函数的单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设集合A={x|-3<x<3},B={y|y=-x2+t},若A∩B=∅,则实数t的取值范围是( )
| A、t≤-3 | B、t<3 |
| C、t>3 | D、t≥3 |
已知数列{an},定直线l:(m+3)x-(2m+4)y-m-9=0,若(n,an)在直线l上,则数列{an}的前13项和为( )
| A、10 | B、21 | C、39 | D、78 |
光线从点A(-2,
)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2
),则光线BC所在直线的倾斜角为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数y=f(x)在区间(a,b)上的导函数为f′(x),f′(x)在区间(a,b)上的导函数为f″(x),若在区间(a,b)上f″(x)>0,则称函数f(x)在区间(a,b)上为“凹函数”,已知f(x)=
x5-
mx4-2x2在区间(1,3)上为“凹函数”,则实数m的取值范围为( )
| 1 |
| 20 |
| 1 |
| 12 |
A、(-∞,
| ||
B、[
| ||
| C、(-∞,-3) | ||
| D、(-∞,5] |
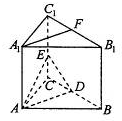 如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.