题目内容
17.设数列{an}的前n项和Sn满足Sn=2an-a1,且a1,a3+1,a4成等差数列,令bn=log2an.(1)求数列{an}的通项公式;
(2)令${c_n}=\frac{b_n}{a_n}$,求数列{cn}的前n项和Tn.
分析 (1)通过Sn=2an-a1与Sn-1=2an-1-a1(n≥2)作差可知an=2an-1(n≥2),利用a1,a3+1,a4成等差数列可知a1=2,从而数列{an}是首项为2,公比为2的等比数列,进而计算可得结论;
(2)通过(1)可知${c_n}=\frac{n}{a_n}=\frac{n}{2^n}$,进而利用错位相减法计算即得结论.
解答 解:(1)由题意,可知Sn=2an-a1,
从而Sn-1=2an-1-a1(n≥2),
上述两式相减,可得Sn-Sn-1=2an-2an-1,
即an=2an-2an-1,
所以an=2an-1(n≥2),
从而a2=2a1,a3=2a2=4a1,a4=2a3=8a1,
又因为a1,a3+1,a4成等差数列,
所以a1+a4=2(a3+1),即a1+8a1=2(4a1+1),
解之得a1=2,
又an=2an-1(n≥2),
所以数列{an}是首项为2,公比为2的等比数列,
故数列{an}的通项公式为${a_n}=2×{2^{n-1}}={2^n}$…(6分)
(2)由(1),可知${c_n}=\frac{n}{a_n}=\frac{n}{2^n}$,
所以${T_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n-1}{{{2^{n-1}}}}+\frac{n}{2^n}$,①
以上等式两边同乘以$\frac{1}{2}$,可得$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{2}{2^3}+…+\frac{n-1}{2^n}+\frac{n}{{{2^{n+1}}}}$,②
由①-②,可得得$\frac{1}{2}{T_n}=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}$
=$\frac{{\frac{1}{2}[1-{{(\frac{1}{2})}^n}]}}{{1-\frac{1}{2}}}-\frac{n}{{{2^{n+1}}}}=1-{(\frac{1}{2})^n}-\frac{n}{{{2^{n+1}}}}$
=$1-\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}=1-\frac{n+2}{{{2^{n+1}}}}$,
所以${T_n}=2-\frac{n+2}{2^n}$…(14分)
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

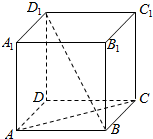 如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.