题目内容
7.设f(x)=loga(1+x)+loga(3-x)(a>0且a≠1),已知f(1)=2.(1)求a的值及f(x)的定义域;
(2)求f(x)的值域.
分析 (1)把已知f(1)=2代入原函数即可求出a的值,再由对数函数的性质列出不等式组,解不等式组则函数的定义域可求;
(2)把已知函数变为f(x)=log2[-(x-1)2+4],再由对数函数的单调性得到函数f(x)在(-1,3)上的最大值,则f(x)的值域可求.
解答 解:(1)∵f(1)=2,∴loga4=2(a>0且a≠1),
∴a=2.
由$\left\{\begin{array}{l}1+x>0\\ 3-x>0\end{array}\right.$,得x∈(-1,3),
∴函数f(x)的定义域为:(-1,3);
(2)f(x)=log2(1+x)+log2(3-x)
=log2(1+x)(3-x)=log2[-(x-1)2+4],
∴当x∈(-1,1]时,f(x)是增函数;
当x∈(1,3)时,f(x)是减函数,
∴函数f(x)在(-1,3)上的最大值是f(1)=log24=2.
∴函数的值域为:(-∞,2).
点评 本题考查了函数的定义域及其求法,考查了函数的值域,是中档题.

练习册系列答案
相关题目
17.正方体的全面积为54,则它的外接球的表面积为( )
| A. | 27π | B. | $\frac{8\sqrt{2}}{3}$π | C. | 36π | D. | $\frac{9\sqrt{3}}{2}$π |
18.已知等差数列{an}的前n项和为Sn,若a3+a4=5,则S6=( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
2.方程y=k(x-1)表示( )
| A. | 过点(-1,0)的所有直线 | B. | 过点(1,0)的所有直线 | ||
| C. | 过点(1,0)且不垂直于x轴的所有直线 | D. | 过点(1,0)且除去x轴的所有直线 |
12.央视记者柴静的《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出表中数据.
(1)请画出表中数据的散点图;(画在答题卷上的坐标纸上)
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归直线方程$\hat y=\hat bx+\hat a$;
(3)试根据(2)求出线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
(相关公式:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\hat a=\overline y-\hat b\overline x$)
| x | 4 | 5 | 7 | 8 |
| y | 2 | 3 | 5 | 6 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归直线方程$\hat y=\hat bx+\hat a$;
(3)试根据(2)求出线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
(相关公式:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\hat a=\overline y-\hat b\overline x$)
19.已知集合A={1,4,x},B={1,x2},且B⊆A,则满足条件的实数x有( )
| A. | 1 个 | B. | 2 个 | C. | 3个 | D. | 4个 |
16.运行如图所示的程序框图,若输出结果为$\frac{15}{8}$,则判断框中应该填的条件是( )
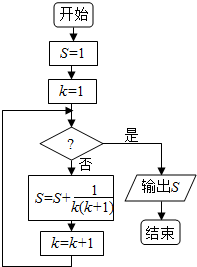

| A. | k>5 | B. | k>6 | C. | k>7 | D. | k>8 |