题目内容

7．已知sinα-cosα=$\frac{1}{5}$，且0＜α＜π，则tanα=$\frac{4}{3}$．

分析 由条件利用同角三角函数的基本关系求得sinαcosα的值以及sinα+cosα的值，从而求得sinα和cosα的值，进而求得tanα的值．

解答 解：∵sinα-cosα=$\frac{1}{5}$，且0＜α＜π，平方可得 1-2sinαcosα=$\frac{1}{25}$，求得sinαcosα=$\frac{12}{25}$，
sinα+cosα=$\sqrt{{（sinα+cosα）}^{2}}$=$\sqrt{1+2sinαcosα}$=$\sqrt{1+\frac{24}{25}}$=$\frac{7}{5}$，
∴sinα=$\frac{4}{5}$，cosα=$\frac{3}{5}$，∴tanα=$\frac{4}{3}$，
故答案为：$\frac{4}{3}$．

点评 本题主要考查同角三角函数的基本关系，属于基础题．

练习册系列答案
相关题目
17．设数列{an}的前n项和Sn满足Sn=2an-a1，且a1，a3+1，a4成等差数列，令bn=log2an．
（1）求数列{an}的通项公式；
（2）令${c_n}=\frac{b_n}{a_n}$，求数列{cn}的前n项和Tn．
18．河水自东向西的流速为3m/s，一轮船以4m/s的速度垂直水流方向向北横渡，求轮船实际航行速度和方向．（参考数据：tan37°≈$\frac{3}{4}$，tan53°=$\frac{4}{3}$）
15．（1）若函数f（x）=$\sqrt{（{a}^{2}-1）{x}^{2}+（a-1）x+\frac{2}{a+1}}$的定义域为R，求实数a的范围；
（2）判断k为何值时，函数f（x）=$\frac{2kx-8}{k{x}^{2}+2kx+1}$的定义域为R．
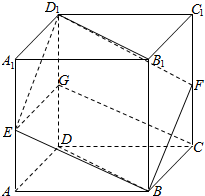2．如图，已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点．
（1）判断多面体EGD1BCF是否是棱柱，并求它的体积；
（2）求证：平面EBFD1⊥平面BB1D1D．
12．F1，F2分别为二次曲线2x2+5y2=30的左，右焦点，动点P满足|PF1|-|PF2|=4，则P点轨迹方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1（x≥2）．
19．函数y=$\sqrt{lo{g}_{\frac{1}{2}}（2-{x}^{2}）}$的定义域是{x|1≤x＜$\sqrt{2}$或-$\sqrt{2}$＜x≤-1}．
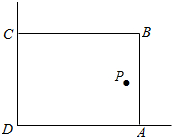16．在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两墙足够长），用16m长的篱笆围成一个矩形花园ABCD（篱笆只围AB、BC两边），在P处有一棵树与墙CD、AD的距离分别是a（0＜a＜12）m和4m，现需要将这棵树围在花园内（含边界，不考虑树的粗细）．设矩形ABCD的面积是ym2，长DA为xm．
（1）设y=f（x），求y=f（x）的解析式并求出其定义域；
（2）试求y=f（x）的最大值与最小值之差g（a）．
17．若f（x）=x${\;}^{\frac{1}{2}}$，则f（$\frac{1}{2}$）=$\frac{\sqrt{2}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网