题目内容
5．在△ABC中，若∠ACB=90°，∠BAC=60°，AB=8，PC⊥平面ABC，PC=4，则$\overrightarrow{PA}•\overrightarrow{PB}$=16．分析 建立如图所示的坐标系，则P（0，0，4），B（4，0，0），A（0，4$\sqrt{3}$，0），利用数量积公式，即可求出$\overrightarrow{PA}•\overrightarrow{PB}$．
解答 
解：建立如图所示的坐标系，则P（0，0，4），B（4，0，0），A（0，4$\sqrt{3}$，0），
∴$\overrightarrow{PA}•\overrightarrow{PB}$=（0，4$\sqrt{3}$，-4）•（4，0，-4）=16．
故答案为：16．
点评 本题考查向量的数量积公式，考查学生的计算能力，正确建立坐标系是关键．
练习册系列答案
阅读快车系列答案
相关题目
16．运行如图所示的程序框图，若输出结果为$\frac{15}{8}$，则判断框中应该填的条件是（ ）
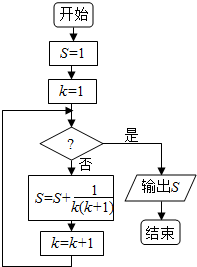
| A． | k＞5 | B． | k＞6 | C． | k＞7 | D． | k＞8 |
13．已知向量$\overrightarrow a$=（sinθ，cosθ），$\overrightarrow b$=（2，-1），若$\overrightarrow a⊥\overrightarrow b$，则cos2θ+sin2θ=（ ）
| A． | -$\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{7}{5}$ |
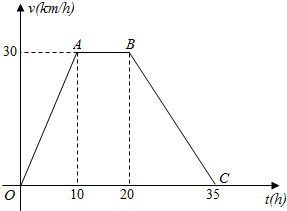据气象中心观察和预测：发生于 地的沙尘暴一直向正南方向移动，其移动速度v（km/h）与时间t的函数图象如图所示，过线段OC 上一点T（t，0）作横轴的垂线l，梯形OABC在直线l 左侧部分的面积即为t（h）内沙尘暴所经过的路程s（km）．