题目内容
8.已知△ABC中,$|\overrightarrow{BC}|=6$,$\overrightarrow{AB}•\overrightarrow{AC}=16$,D为边BC的中点,则$|\overrightarrow{AD}|$=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 运用向量的加减运算可得,$\overrightarrow{AB}$•$\overrightarrow{AC}$=($\overrightarrow{AD}$+$\overrightarrow{DB}$)•($\overrightarrow{AD}$+$\overrightarrow{DC}$),再由向量的数量积的性质,计算即可得到所求值.
解答  解:$\overrightarrow{AB}$=$\overrightarrow{AD}$+$\overrightarrow{DB}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$,
解:$\overrightarrow{AB}$=$\overrightarrow{AD}$+$\overrightarrow{DB}$,$\overrightarrow{AC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$,
即有$\overrightarrow{AB}$•$\overrightarrow{AC}$=($\overrightarrow{AD}$+$\overrightarrow{DB}$)•($\overrightarrow{AD}$+$\overrightarrow{DC}$)
=$\overrightarrow{AD}$2+$\overrightarrow{AD}$•($\overrightarrow{DB}$+$\overrightarrow{DC}$)+$\overrightarrow{DB}$•$\overrightarrow{DC}$
=|$\overrightarrow{AD}$|2+0-|$\overrightarrow{DB}$|•|$\overrightarrow{DC}$|=16,
即有|$\overrightarrow{AD}$|2=16+3×3=25,
解得$|\overrightarrow{AD}|$=5.
故选C.
点评 本题考查向量的数量积的定义和性质,考查向量的平方即为模的平方,考查向量的加减运算,属于基础题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
| A. | 1 个 | B. | 2 个 | C. | 3个 | D. | 4个 |
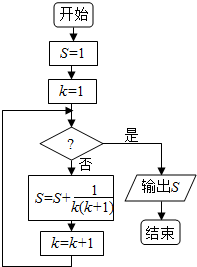
| A. | k>5 | B. | k>6 | C. | k>7 | D. | k>8 |
| A. | 向左平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
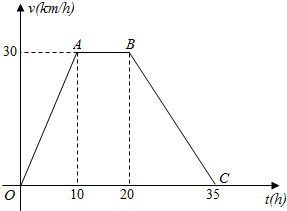 据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).