题目内容
已知定义在R上的函数f(x)=-f(x+
),且f(-2)=f(-1)=-1,f(0)=2,f(1)+f(2)+…+f(2009)+f(2010)= .
| 3 |
| 2 |
考点:函数的周期性
专题:函数的性质及应用
分析:根据题意可推出f(x)=f(x+3),结合f(-2)=f(-1)=-1,f(0)=2,利用分组求和法可得答案.
解答:
解:f(x)=-f(x+
),
∴f(x+3)=f[(x+
)+
]=-f(x+
)=f(x),
故函数f(x)是以3为周期的周期函数,
又∵(-2)=f(-1)=-1,f(0)=2,
∴f(1)=-1,f(2)=-1,f(3)=2,
即f(1)+f(2)+f(3)=0,
故f(1)+f(2)+…+f(2009)+f(2010)=670×[f(1)+f(2)+f(3)]=0,
故答案为:0
| 3 |
| 2 |
∴f(x+3)=f[(x+
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故函数f(x)是以3为周期的周期函数,
又∵(-2)=f(-1)=-1,f(0)=2,
∴f(1)=-1,f(2)=-1,f(3)=2,
即f(1)+f(2)+f(3)=0,
故f(1)+f(2)+…+f(2009)+f(2010)=670×[f(1)+f(2)+f(3)]=0,
故答案为:0
点评:本题考查函数的周期性,及求函数值,推出f(x)=f(x+3),是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知复数z=
,i是虚数单位,则复数虚部是( )
| 1+2i |
| 3-i |
A、
| ||
B、
| ||
C、
| ||
D、
|
集合A={x∈N|3<x<9},B={3,5,7,8},则A∪B中的元素的个数有( )
| A、0 | B、2 | C、4 | D、6 |
由二项式定理知识可将[(x+y)n-(x-y)n](n∈N*)展开并化简.若a=
(
)dx,则在(a+5)2n+1(n∈N*)的小数表示中,小数点后面至少连续有零的个数是( )
| ∫ | 26 0 |
| 1 | ||
2
|
| A、2n-1 | B、2n |
| C、2n+1 | D、2n+2 |
下列函数中,满足f(xy)=f(x)+f(y)的单调递增函数是( )
| A、f(x)=log2x | ||
| B、f(x)=x2 | ||
| C、f(x)=2x | ||
D、f(x)=log
|
若不等式ax2+bx+c<0的解集为{x|x<0或x>β},(α<β<0),则不等式cx2-bx+a>0的解集为( )
A、{x|-
| ||||
B、{x|
| ||||
C、{x|-
| ||||
D、{x|x<-
|
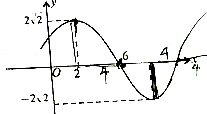 函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.
函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.