题目内容
已知命题p:|1-
|≤2 命题q:x2-2x+1-m2≤0(m>0),且p是q的必要而不充分条件,求实数m的取值范围.
| x-1 |
| 3 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:解绝对值不等式求出满足p的集合P,解二次不等式求出满足q的信Q,进而根据p是q的必要而不充分条件,可得Q?P,进而得到实数m的取值范围.
解答:
解:解|1-
|≤2得:P=[-2,10],
解x2-2x+1-m2≤0得:[1-m,1+m],
若p是q的必要而不充分条件,
则Q?P,
则1-m≥-2且1+m≤10,
解得m≤3,
又由m>0,
∴实数m的取值范围为(0,3]
| x-1 |
| 3 |
解x2-2x+1-m2≤0得:[1-m,1+m],
若p是q的必要而不充分条件,
则Q?P,
则1-m≥-2且1+m≤10,
解得m≤3,
又由m>0,
∴实数m的取值范围为(0,3]
点评:本题考查的知识点是充要条件的定义,二次不等式的解法,绝对值不等式的解法,集合的包含关系,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a∈R,则“a=1”是直线“l1:ax+2y-1=0与直线l2:(a+1)x-y+4=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
已知变量x,y之间具有相关关系,其散点图如图所示,则其回归直线方程可能是( )
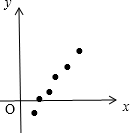

| A、y=2x-1 |
| B、y=2x+1 |
| C、y=-2x+1 |
| D、y=-2x-1 |
函数f(x)满足f(-1)=
,对于x,y∈R,有4f(
)f(
)=f(x)+f(y),则f(-2013)=( )
| 1 |
| 4 |
| x+y |
| 2 |
| x-y |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|