题目内容
求函数y=sin（2x+
）在[0，π]内的单调增区间．
| π |
| 3 |
考点：正弦函数的单调性
专题：三角函数的图像与性质
分析：根据条件求出函数的递增区间即可得到结论．
解答：
解：∵y=sin（2x+
），
∴由2kπ-
≤2x+
≤2kπ+
，k∈Z．
得kπ-
≤x≤kπ+
，k∈Z．
∴当k=0时，递增区间为[0，
]，
当k=1时，递增区间为[
，π]，
即在[0，π]内的单调增区间是[0，
]和[
，π]．
| π |
| 3 |
∴由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得kπ-
| 5π |
| 12 |
| π |
| 12 |
∴当k=0时，递增区间为[0，
| π |
| 12 |
当k=1时，递增区间为[
| 7π |
| 12 |
即在[0，π]内的单调增区间是[0，
| π |
| 12 |
| 7π |
| 12 |
点评：本题主要考查正弦函数的单调性的应用，要求熟练掌握三角函数的图象和性质．
练习册系列答案
相关题目
已知cos（α+
）=
，α∈（-
，0），则tan（2π-α）=（ ）
| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
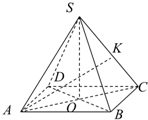如图，设S-ABCD是一个高为3的四棱锥，底面ABCD是边长为2的正方形，顶点S在底面上的射影是正方形ABCD的中心．K是棱SC的中点．试求直线AK与平面SBC所成角的大小．