题目内容
双曲线x2+ay2=1的一条渐近线的方程为2x+3y=0，则a= ．
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：通过双曲线方程求出渐近线方程，与已知方程比较即可求出a的值．
解答：
解：双曲线x2+ay2=1，∴a＜0．
双曲线x2+ay2=1的渐近线是x=±
y，
又双曲线x2+ay2=1的一条渐近线的方程为2x+3y=0，
可知
=
，
∴a=-
．
故答案为：-
．
双曲线x2+ay2=1的渐近线是x=±
| -a |
又双曲线x2+ay2=1的一条渐近线的方程为2x+3y=0，
可知
| -a |
| 3 |
| 2 |
∴a=-
| 9 |
| 4 |
故答案为：-
| 9 |
| 4 |
点评：本题考查双曲线的基本性质的应用，渐近线方程的求法，考查计算能力．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
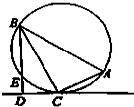如图，在△ABC中，∠C=90°，∠A=60°，过C作△ABC的外接圆的切线CD，BD⊥CD于D．BD与外接圆交于点E，已知DE=5，则△ABC的外接圆的半径为
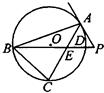如图，△ABC是圆O的内接三角形，PA是圆O的切线，PB交AC于点E，交圆O于点D，若PA=PE，PB=9，PD=1，∠ABC=60°，则EC的长等于设a，b∈R，则“a3＜b3”是“a＜b”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若△ABC为锐角三角形，则下列不等式中一定能成立的是（ ）
A、logcosC
| ||
B、logcosC
| ||
C、logsinC
| ||
D、logsinC
|