题目内容
9.等比数列{an}中,若a2a5=2a3,a4与a6的等差中项为$\frac{5}{4}$,则a1=±16.分析 设等比数列{an}的公比为q.由a2a5=2a3,可得${a}_{1}^{2}{q}^{5}$=2a1q2,化为:${a}_{1}{q}^{3}$=2=a4.由a4与a6的等差中项为$\frac{5}{4}$,可得a4+a6=2×$\frac{5}{4}$,即${a}_{4}(1+{q}^{2})$=$\frac{5}{2}$.代入解出即可得出.
解答 解:设等比数列{an}的公比为q.
∵a2a5=2a3,
∴${a}_{1}^{2}{q}^{5}$=2a1q2,化为:${a}_{1}{q}^{3}$=2=a4.
∵a4与a6的等差中项为$\frac{5}{4}$,∴a4+a6=2×$\frac{5}{4}$,
∴${a}_{4}(1+{q}^{2})$=$\frac{5}{2}$.
∴q2=$\frac{1}{4}$,解得q=$±\frac{1}{2}$.
则a1×$(±\frac{1}{8})$=2,解得a1=±16.
故答案为:±16.
点评 本题考查了等差数列与等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.已知数列{an}是等差数列且满足a1=1,a3=7,设Sn为数列{(-1)nan}的前n项和,则S2017为( )
| A. | -3025 | B. | -3024 | C. | 2017 | D. | 9703 |
17.等比数列{an},若a12=4,a18=8,则a36为( )
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
14.设函数f(x)=(x-a)2+(ln x2-2a)2,其中x>0,a∈R,存在x0使得f(x0)≤b成立,则实数b的最小值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
18.复数z=|($\sqrt{3}$-i)i|+i2017(i为虚数单位),则复数z的共轭复数为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
19.设函数f(x)=ex(x3-a)(a∈R)在(-3,0)单调递减,则a的范围是( )
| A. | [0,+∞) | B. | [2,4] | C. | [4,+∞) | D. | (2,4) |
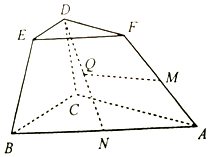 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.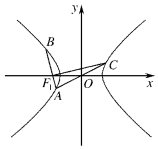 如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.