题目内容
6.已知函数f(x)=|x+2|+|x-2|.(1)求不等式f(x)≤6的解集A;
(2)若m,n∈A,试证:|${\frac{1}{3}$m-$\frac{1}{2}$n|≤$\frac{5}{2}$.
分析 (1)分类讨论,即可求不等式f(x)≤6的解集A;
(2)利用绝对值不等式,即可证明结论.
解答 (1)解:不等式|x+2|+|x-2|≤6可以转化为$\left\{{\begin{array}{l}{x≤-2}\\{-({x+2})-({x-2})≤6}\end{array}}\right.$或$\left\{{\begin{array}{l}{-2<x≤2}\\{({x+2})-({x-2})≤6}\end{array}}\right.$
或$\left\{{\begin{array}{l}{x>2}\\{({x+2})+({x-2})≤6}\end{array}}\right.$,
解得-3≤x≤3,
即不等式的解集A={x|-3≤x≤3}.
(2)证明:因为$|{\frac{1}{3}m-\frac{1}{2}n}|≤|{\frac{1}{3}m}|+|{\frac{1}{2}n}|=\frac{1}{3}|m|+\frac{1}{2}|n|$,
又因为m,n∈A,所以|m|≤3,|n|≤3,
所以$\frac{1}{3}|m|+\frac{1}{2}|n|≤\frac{1}{3}×3+\frac{1}{2}×3=\frac{5}{2}$,当且仅当m=-n=±3时,等号成立,
即$|{\frac{1}{3}m-\frac{1}{2}n}|≤\frac{5}{2}$,得证.
点评 本题考查不等式的解法与证明,考查绝对值不等式的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
14.已知角α的顶点与坐标原点重合,始边与x轴的非负半轴重合,终边经过点P(1,-2),则sin2α=( )
| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
5.函数y=2xex的一个原函数为( )
| A. | 2xex(1+ln2) | B. | $\frac{{2}^{x}{e}^{x}}{(1+ln2)}$ | C. | 2exln2 | D. | $\frac{2{e}^{x}}{ln2}$ |
12.设x1,x2为f(x)=sin(ωx-$\frac{π}{6}$)(ω>0)的两个零点,且|x2-x1|的最小值为1,则ω=( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
10.椭圆$C:\frac{x^2}{4}+\frac{y^2}{3}=1$与双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a,b>0)$有相同的焦点,且两曲线的离心率互为倒数,则双曲线渐近线的倾斜角的正弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
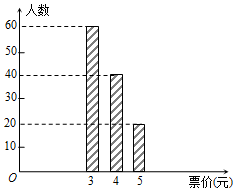 已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.