题目内容
4.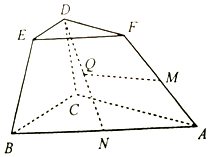 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.(Ⅰ)设ND中点为Q,$λ=\frac{1}{2}$,求证:MQ∥平面ABC;
(Ⅱ)若M到平面BCD的距离为$\frac{{3\sqrt{3}}}{4}$,求直线MC与平面BCD所成角的正弦值.
分析 (Ⅰ)延长三棱台的三条侧棱,设交点为S,当$λ=\frac{1}{2}$时M为FA的中点,设CD中点为R,连MR,MQ,RQ,由中位线定理可证MR∥平面ABC,QR∥平面ABC,再由面面平行的判定可得平面MQR∥平面ABC,从而得到MQ∥平面ABC;
(Ⅱ)设AB中点为H,连SH,AH,在△SAH中,作MO∥AH且交SH于点O,由平面ABC⊥平面BCDE,可得AH⊥平面SBC,进一步得到MO⊥平面SBC(D),求出M到平面SBC的距离MO.可得∠MCO为直线MC与平面BCD所成角.然后求解三角形得答案.
解答 (Ⅰ)证明:延长三棱台的三条侧棱,设交点为S,当$λ=\frac{1}{2}$时M为FA的中点,
设CD中点为R,连MR,MQ,RQ,
在梯形ACDF中,中位线MR∥AC,又MR?平面ABC,AC?平面ABC,
∴MR∥平面ABC;
在△CDN中,中位线QR∥CN,又QR?平面ABC,CN?平面ABC,
∴QR∥平面ABC,
又MR∩QR=R且MR?平面MQR,QR?平面MQR,
∴平面MQR∥平面ABC,
又MQ?平面MQR
∴MQ∥平面ABC;
(Ⅱ)解:设AB中点为H,连SH,AH,在△SAH中,作MO∥AH且交SH于点O,
∵平面ABC⊥平面BCDE,平面ABC∩平面BCDE=BC,
AH?平面ABC,AH⊥BC,∴AH⊥平面SBC,
又MO∥AH,∴MO⊥平面SBC(D),
∴MO为M到平面SBC的距离,MO=$\frac{3\sqrt{3}}{4}$.
且∠MCO为直线MC与平面BCD所成角.
∵平面ABC⊥平面BCDE,平面ABC∩平面BCDE=BC,
CD?平面BCDE,CD⊥BC,∴CD⊥平面ABC,
又AC?平面ABC,∴CD⊥AC,
在Rt△SAC中,DF∥AC,DF=1,AC=2,CD=1,
由$\frac{MO}{AH}=\frac{\frac{3\sqrt{3}}{4}}{\sqrt{3}}=\frac{3}{4}$,得$\frac{SM}{SA}=\frac{3}{4}$,即M为FA的中点.
∴CF⊥SA,又CF=$\sqrt{2}$,FM=$\frac{\sqrt{2}}{2}$,∴CM=$\frac{\sqrt{10}}{2}$.
在Rt△MCO中,sin∠MCO=$\frac{MO}{MC}=\frac{3\sqrt{30}}{20}$.
故直线MC与平面BCD所成角的正弦值为$\frac{{3\sqrt{30}}}{20}$.
点评 本题考查直线与平面平行的判定,考查线面角的求法,考查空间想象能力与思维能力,是中档题.

| A. | m+n=0 | B. | m-n=0 | C. | mn+1=0 | D. | mn-1=0 |
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
| A. | (2,+∞) | B. | (1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{4}$,+∞) |
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{2}$ |