题目内容
14. 如图,等腰三角形ABC中,∠B=∠C,D在BC上,∠BAD大小为α,∠CAD大小为β.
如图,等腰三角形ABC中,∠B=∠C,D在BC上,∠BAD大小为α,∠CAD大小为β.(1)若$α=\frac{π}{4},β=\frac{π}{3}$,求$\frac{BD}{DC}$;
(2)若$\frac{BD}{DC}=\frac{1}{2},β=α+\frac{π}{3}$,求∠B.
分析 (1)分别在△ABD和△ACD中使用正弦定理即可得出$\frac{BD}{DC}=\frac{sinα}{sinβ}$;
(2)利用三角恒等变换求出α,从而得出∠B.
解答 解:(1)在△ABD中,由正弦定理得$\frac{BD}{sinα}=\frac{AD}{sinB}$,
在△ACD中,由正弦定理得$\frac{DC}{sinβ}=\frac{AD}{sinC}$,
∵∠B=∠C,
∴$\frac{BD}{sinα}=\frac{DC}{sinβ}$,
∴$\frac{BD}{DC}=\frac{sinα}{sinβ}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{{\sqrt{6}}}{3}$.
(2)由(1)知$\frac{BD}{DC}$=$\frac{sinα}{sinβ}$=$\frac{1}{2}$,
又β=α+$\frac{π}{3}$,∴sinβ=sin($α+\frac{π}{3}$)=$\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα,
∴$\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα=2sinα,即$\sqrt{3}$cosα=3sinα,
∴tanα=$\frac{\sqrt{3}}{3}$,∴α=$\frac{π}{6}$,β=$\frac{π}{2}$,
∴B=$\frac{1}{2}$(π-α-β)=$\frac{π}{6}$.
点评 本题考查了正弦定理,三角恒等变换,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
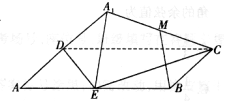 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中: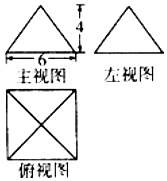 已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.
已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.