题目内容
19．已知k是正整数，且1≤k≤2017，则满足方程sin1°+sin2°+…+sink°=sin1°•sin2°…sink°的k有11个．分析 由三角函数的值域可知，除k=1外当等式sin1°+sin2°+…+sink°=sin1°•sin2°…sink°的左右两边均为0时等式成立，由此可得正整数k的个数．
解答 解：由三角函数的单调性及值域，可知sin1°•sin2°…sink°＜1．
∴除k=1外只有当等式sin1°+sin2°+…+sink°=sin1°•sin2°…sink°的左右两边均为0时等式成立，
则k=1、359、360、719、720、1079、1080、1439、1440、1799、1800时等式成立，
满足条件的正整数k有11个．
故答案为：11．
点评 本题考查三角函数的化简求值，寻找规律是解答该题的关键，是基础题．
练习册系列答案
相关题目
9．已知动点M到点A（2，0）的距离是它到点B（8，0）的距离一半，则动点M的轨迹方程是（ ）
| A． | （x-2）2+y2=16 | B． | x2+y2=16 | C． | （x-4）2+y2=16 | D． | x2+y2=4 |
10．已知$sinα+cosα=\frac{1}{5}$，且$-\frac{π}{2}≤α≤\frac{π}{2}$，那么tanα等于（ ）
| A． | $-\frac{4}{3}$ | B． | $-\frac{3}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
7．
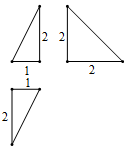已知某三棱锥的三视图如图所示，图中的3个直角三角形的直角边长度已经标出，则在该三棱锥中，最短的棱和最长的棱所在直线的成角余弦值为（ ）
已知某三棱锥的三视图如图所示，图中的3个直角三角形的直角边长度已经标出，则在该三棱锥中，最短的棱和最长的棱所在直线的成角余弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
如图，等腰三角形ABC中，∠B=∠C，D在BC上，∠BAD大小为α，∠CAD大小为β．
4．若函数f（x）=a3-cosx，则f'（a）=（ ）
| A． | 3a2+sina | B． | 3a2-sina | C． | sina | D． | cosa |
11．设集合M={x|x2＞4}，N={x|x＜3}，则以下各式正确的是（ ）
| A． | M∪N={x|x＜3} | B． | M∩N={x|2＜|x|＜3} | C． | M∩N={x|2＜x＜3} | D． | M∪N=R |