题目内容
杜拉拉因卓越的表现,每两年一晋升,工资也相应的得到提高,在公司,她的工资成了同事谈论的焦点,本报记者从DB公司获取杜拉拉这几年工资清单表,列表如下,如果杜拉拉计划在其事业的第四阶段年收入为40万,那么下列三个函数,二次函数f(x)=ax2+bx+c(a≠0),指数型函数g(x)=a•bx+c,对数型函数h(x)=a•lnx+b,哪一个是最佳模拟函数模型?
| 阶段 | 职位 | 工资(年收入) |
| 第一阶段(29岁) | 销售总监秘书 | 8万 |
| 第二阶段(31岁) | HR主管 | 18万 |
| 第三阶段(33岁) | HR经理 | 30万 |
考点:根据实际问题选择函数类型
专题:函数的性质及应用
分析:设29岁为1,31岁为2,33岁为3,则对应坐标为(1,8),(2,18),(3,30),分别求三个函数的表达式,即可解得.
解答:
解:建立年销量(万辆)与第x年的函数,
设29岁为1,31岁为2,33岁为3,则对应坐标为(1,8),(2,18),(3,30),
可知函数图象必过点(1,8),(2,18),(3,30).
(1)将点的坐标代入二次函数型f(x)=ax2+bx+c(a≠0),可得
,
解得a=1,b=7,c=0,
则f(x)=x2+7x,故f(4)=44,与计划误差为4.
(2)构造指数函数型g(x)=a•bx+c(a≠0,b≠1,b>0),将点的坐标代入,可得
解得a=
,b=
,c=-42,
则g(x)=
•(
)x-42.
故g(4)=44.4,与计划误差为4.4.
由上可得f(x)=x2+7x模型能更好地反映该公司年销量与第x年的关系.
(3).若h(x)=a•lnx+b,
则
,此时若a存在,
则h(4)=aln4+b=2aln2+8=28,与40相差40-28=12,
综上二次函数f(x)=ax2+bx+c(a≠0)是最佳模拟函数模型.
设29岁为1,31岁为2,33岁为3,则对应坐标为(1,8),(2,18),(3,30),
可知函数图象必过点(1,8),(2,18),(3,30).
(1)将点的坐标代入二次函数型f(x)=ax2+bx+c(a≠0),可得
|
解得a=1,b=7,c=0,
则f(x)=x2+7x,故f(4)=44,与计划误差为4.
(2)构造指数函数型g(x)=a•bx+c(a≠0,b≠1,b>0),将点的坐标代入,可得
|
解得a=
| 125 |
| 3 |
| 6 |
| 5 |
则g(x)=
| 125 |
| 3 |
| 6 |
| 5 |
故g(4)=44.4,与计划误差为4.4.
由上可得f(x)=x2+7x模型能更好地反映该公司年销量与第x年的关系.
(3).若h(x)=a•lnx+b,
则
|
则h(4)=aln4+b=2aln2+8=28,与40相差40-28=12,
综上二次函数f(x)=ax2+bx+c(a≠0)是最佳模拟函数模型.
点评:本题主要考查函数模型的应用,利用待定系数法分别求出对应的系数,进行误差判断是解决本题的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
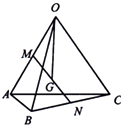 已知空间四边形OABC,M,N分别是OA,BC的中点,点G是线段MN的中点,设
已知空间四边形OABC,M,N分别是OA,BC的中点,点G是线段MN的中点,设| OG |
| OA |
| OB |
| OC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|