题目内容
已知区域E={(x,y)|0≤x≤4,0≤y≤2},F={(x,y)|0≤x≤4,0≤y≤2,x≥y},若向区域E内随机投掷一点,则该点落入区域F内的概率为 .
考点:几何概型
专题:应用题,概率与统计
分析:本问题属于几何概型,求出相应的面积,即可求出概率.
解答:
 解:依题意可知,本问题属于几何概型,区域E和区域F的对应图形如图所示.
解:依题意可知,本问题属于几何概型,区域E和区域F的对应图形如图所示.
其中区域E的面积为4×2=8,区域F的面积为
×(2+4)×2=6,
所以向区域E内随机投掷一点,该点落入区域F内的概率为
.
故答案为:
.
 解:依题意可知,本问题属于几何概型,区域E和区域F的对应图形如图所示.
解:依题意可知,本问题属于几何概型,区域E和区域F的对应图形如图所示.其中区域E的面积为4×2=8,区域F的面积为
| 1 |
| 2 |
所以向区域E内随机投掷一点,该点落入区域F内的概率为
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查的知识点是几何概型的意义.几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
下列命题正确的是( )
| A、垂直于同一直线的两条直线互相平行 |
| B、平行四边形在一个平面上的平行投影一定是平行四边形 |
| C、锐角三角形在一个平面上的平行投影不可能是钝角三角形 |
| D、平面截正方体所得的截面图形不可能是正五边形 |
在如图所示的程序框图中,若f0(x)=xex,则输出的结果是( )
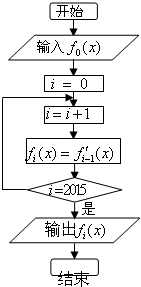

| A、2016ex+xex |
| B、2015ex+xex |
| C、2014ex+xex |
| D、2013ex+x |